/Szkoła średnia/Równania/Trygonometryczne/Stopnia 1

Zadanie nr 4550983

Rozwiąż równanie 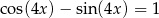cos(4x )− sin(4x ) = 1 .

Wersja PDF

Rozwiązanie

Sposób I

Będziemy chcieli skorzystać ze wzoru

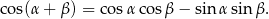
co s(α+ β) = cos αco sβ − sin αsin β.

W tym celu mnożymy obie strony przez 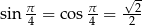π π √ 2 sin 4-= cos-4 = -2-

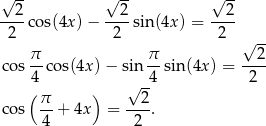
√ -- √ -- √ -- --2-cos(4x) − --2-sin(4x) = --2- 2 2 2 -- π π √ 2 cos --cos(4x )− sin --sin(4x ) = ---- 4 √ -4 2 (π- ) --2- cos 4 + 4x = 2 .

I dalej już łatwo,

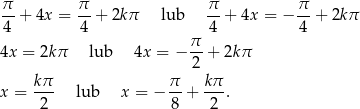
π- + 4x = π-+ 2kπ lub π-+ 4x = − π-+ 2kπ 4 4 4 4 π- 4x = 2kπ lub 4x = − 2 + 2kπ kπ π kπ x = --- lub x = − -- + ---. 2 8 2

Sposób II

Chcemy skorzystać ze wzoru

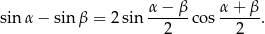
sin α − sinβ = 2 sin α-−-β-cos α-+-β-. 2 2

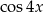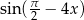W tym celu zamienimy co s4x na sin( π2-− 4x) .

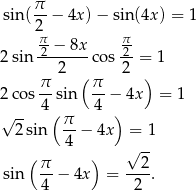
π sin (--− 4x)− sin (4x) = 1 2π π 2-−-8x- 2- 2 sin 2 cos 2 = 1 π ( π ) 2 cos 4-sin 4-− 4x = 1 √ -- ( π ) 2 sin --− 4x = 1 4 √ -- ( π- ) --2- sin 4 − 4x = 2 .

Ponieważ

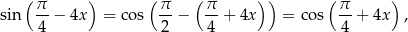
( ) ( ( ) ) ( ) sin π-− 4x = cos π-− π- + 4x = co s π-+ 4x , 4 2 4 4

otrzymane równanie jest identyczne z tym otrzymanym w sposobie I.

Sposób III

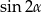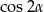Przekształcamy równanie korzystając ze wzorów na sin 2α i cos2α .

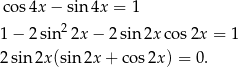
cos4x − sin 4x = 1 1 − 2 sin22x − 2 sin2x cos 2x = 1 2 sin2x (sin 2x + co s2x) = 0 .

Mamy zatem 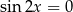sin2x = 0 , czyli 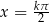x = kπ2- lub

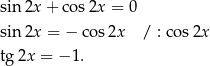
sin 2x + co s2x = 0 sin 2x = − cos 2x / : cos2x tg 2x = − 1.

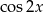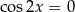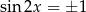Po drodze dzieliliśmy przez co s2x , ale nie z tym problemu, bo jeżeli cos2x = 0 to sin 2x = ±1 i powyższe równanie jest sprzeczne. Otrzymujemy więc dodatkowo

π- π- kπ- 2x = − 4 + kπ ⇐ ⇒ x = − 8 + 2 .

 
Odpowiedź: x = kπ- lub x = − π-+ kπ- 2 8 2

Wersja PDF