Zadanie nr 4975504

Rozwiąż równanie 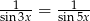--1-- --1-- sin3x = sin5x w przedziale ⟨ π-π-⟩ − 2,2 .

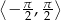Rozwiązanie

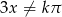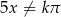Na początku zauważmy, że mianowniki muszą być niezerowe, czyli 3x ⁄= kπ i 5x ⁄= kπ . Po uwzględnieniu podanej dziedziny daje to nam

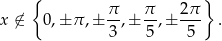
{ } x ⁄∈ 0,± π,± π-,± π-,± 2-π . 3 5 5

Sposób I

Korzystamy ze wzoru na różnicę sinusów

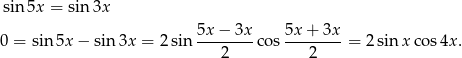
sin 5x = sin 3x 0 = sin 5x − sin 3x = 2 sin 5x-−--3x cos 5x-+-3x = 2 sinx cos 4x. 2 2

Zatem

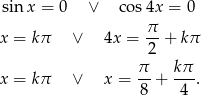
sin x = 0 ∨ cos4x = 0 π x = kπ ∨ 4x = -- + kπ 2 x = kπ ∨ x = π-+ kπ-. 8 4

Uwzględniając ograniczenie 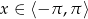x ∈ ⟨− π ,π⟩ oraz dziedzinę równania daje to nam rozwiązania

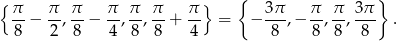
{ } { π- π- π- π- π- π- π} 3π- π- π- 3-π 8 − 2, 8 − 4, 8, 8 + 4 = − 8 ,− 8, 8, 8 .

Sposób II

Korzystamy z następującej równoważności

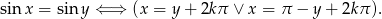
sin x = sin y ⇐ ⇒ (x = y + 2k π ∨ x = π − y+ 2kπ ).

Korzystając z powyższego warunku mamy

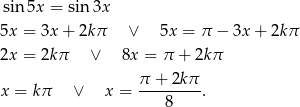
sin5x = sin 3x 5x = 3x + 2k π ∨ 5x = π − 3x + 2kπ 2x = 2kπ ∨ 8x = π + 2kπ π + 2kπ x = kπ ∨ x = ---------. 8

Podobnie jak w poprzednim sposobie, po uwzględnieniu warunku 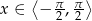⟨ π π ⟩ x ∈ − 2,-2 oraz dziedziny otrzymujemy rozwiązania

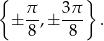
{ } ± π,± 3π- . 8 8

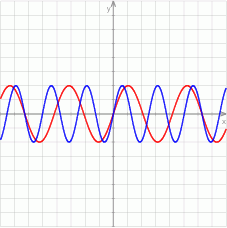
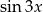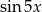Na koniec, dla ciekawskich, wykresy sin 3x i sin 5x (szukaliśmy punktów wspólnych tych wykresów).

Odpowiedź: { } − 3π8-,− π8, π8-, 3π8