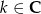Zadanie nr 5445984
Rozwiąż równanie 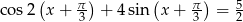 .
.
Rozwiązanie
Korzystając ze wzoru
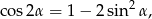
mamy
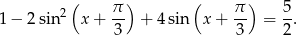
Po podstawieniu 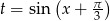 , mamy
, mamy
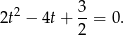
Dalej, 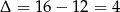 ,
, 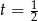 lub
lub 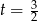 . Drugi z pierwiastków odrzucamy, bo
. Drugi z pierwiastków odrzucamy, bo 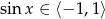 . Zatem
. Zatem 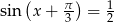 , czyli
, czyli
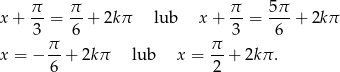
Odpowiedź: 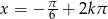 lub
lub 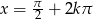 ,
, 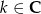
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 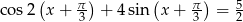 .
.
Korzystając ze wzoru
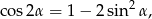
mamy
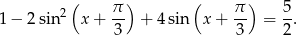
Po podstawieniu 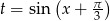 , mamy
, mamy
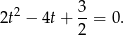
Dalej, 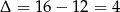 ,
, 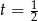 lub
lub 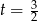 . Drugi z pierwiastków odrzucamy, bo
. Drugi z pierwiastków odrzucamy, bo 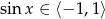 . Zatem
. Zatem 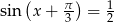 , czyli
, czyli
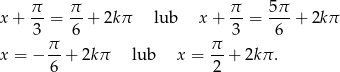
Odpowiedź: 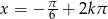 lub
lub 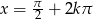 ,
,