/Szkoła średnia/Równania/Trygonometryczne/Stopnia 1

Zadanie nr 5722557

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 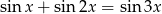sinx + sin 2x = sin 3x .

Rozwiązanie

Korzystamy ze wzorów na sumę sinusów i na 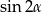sin 2α .

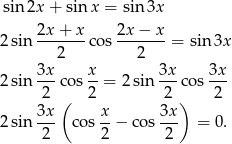
sin 2x + sinx = sin 3x 2x-+-x- 2x-−-x- 2 sin 2 co s 2 = sin3x 3x x 3x 3x 2 sin ---co s--= 2sin ---cos --- 2 ( 2 2 ) 2 2 sin 3x- cos x-− cos 3x- = 0. 2 2 2

Jeżeli 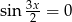sin 3x= 0 2 to mamy

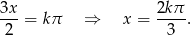
3x-= kπ ⇒ x = 2k-π . 2 3

Teraz zajmujemy się wyrażeniem w nawiasie.

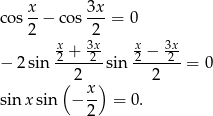
cos x-− cos 3x-= 0 2 2 x + 3x- x − 3x − 2 sin 2----2-sin 2----2-= 0 ( 2x ) 2 sin x sin − -- = 0. 2

Powinno być jasne, że wystarczy zająć się warunkiem 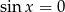sin x = 0 , bo warunek 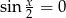x sin 2 = 0 i tak implikuje 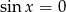sin x = 0 (np. ze wzoru na 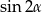sin 2α ). Zatem

x = kπ.

 
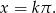
Odpowiedź: 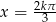x = 2k3π lub x = kπ

Wersja PDF