/Szkoła średnia/Równania/Trygonometryczne/Stopnia 1

Zadanie nr 6421543

Rozwiąż równanie 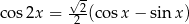√2- cos 2x = 2 (cos x− sin x) w przedziale ⟨0,π ⟩ .

Wersja PDF

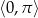Rozwiązanie

Sposób I

Skorzystamy ze wzoru na cosinus sumy

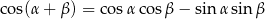
cos(α + β) = cosα cosβ − sin α sin β

Dane równanie możemy więc zapisać w postaci

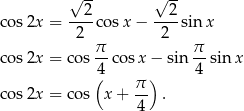
√ -- √ -- co s2x = --2co sx − --2-sin x 2 2 π- π- co s2x = co s 4 cosx − sin 4 sinx ( π ) co s2x = co s x + 4- .

Szkicujemy cosinusa.

PIC

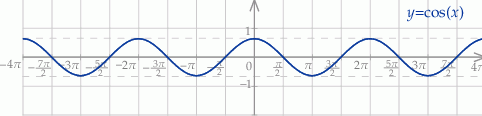
Z wykresu widać, że

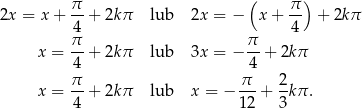
π- ( π-) 2x = x+ 4 + 2kπ lub 2x = − x+ 4 + 2kπ π π x = --+ 2kπ lub 3x = − --+ 2kπ 4 4 x = π-+ 2kπ lub x = − π--+ 2-kπ . 4 12 3

Łatwo teraz sprawdzić, że w przedziale 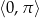⟨0,π⟩ daje to nam dwa rozwiązania

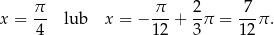
π π 2 7 x = -- lub x = − ---+ -π = ---π. 4 12 3 12

Sposób II

Skorzystamy ze wzoru

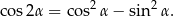
cos 2α = cos2 α− sin 2α.

Przekształcamy dane równanie w sposób równoważny

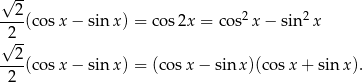
√ -- 2 2 2 ----(cosx − sin x) = cos 2x = cos x− sin x √2-- --2- 2 (cosx − sin x) = (cos x− sin x)(cos x + sin x).

Jeżeli 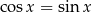cos x = sin x , to oczywiście obie strony muszą być niezerowe i możemy ten warunek zapisać w postaci

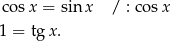
cosx = sin x / : cosx 1 = tg x.

Szkicujemy tangensa.

PIC

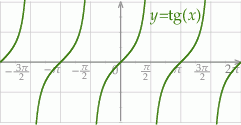
Z wykresu łatwo odczytać, że jedynym rozwiązaniem jest 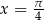π- x = 4 (bo x ∈ ⟨0 ,π⟩ ).

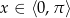Jeżeli natomiast 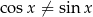cosx ⁄= sin x , to możemy obie strony równania podzielić przez 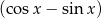(co sx − sinx ) i otrzymujemy równanie

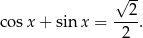
√ -- 2 cos x+ sin x = ---. 2

W tym miejscu będzie chcieli skorzystać ze wzoru na sinus sumy

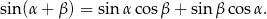
sin (α+ β) = sinα cos β+ sin β cos α.

Mamy zatem

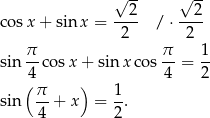
√ -- √ -- cosx + sin x = --2- / ⋅--2- 2 2 π- π- 1- sin 4 c osx + sin xcos 4 = 2 ( π ) 1 sin --+ x = --. 4 2

Szkicujemy sinusa.

PIC

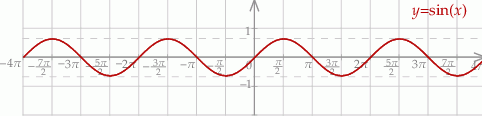
Odczytując rozwiązanie z wykresu musimy trochę uważać, bo wprawdzie 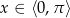x ∈ ⟨0 ,π⟩ , ale

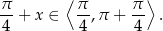
π ⟨π π ⟩ --+ x ∈ --,π + -- . 4 4 4

Mamy zatem

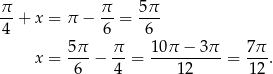
π π 5 π -- + x = π − -- = --- 4 6 6 x = 5π-− π-= 10π-−--3π-= 7π-. 6 4 12 1 2

Wyjściowe równanie ma więc dwa rozwiązania

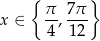
{ } x ∈ π-, 7π 4 1 2

Sposób III

Tak jak w poprzednim sposobie zauważamy, że albo 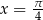π x = 4- , albo

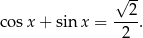
√ -- cos x+ sin x = --2. 2

Tym razem skorzystamy jednak ze wzoru na sumę sinusów

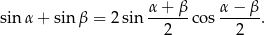
α + β α − β sin α + sinβ = 2 sin ------cos ------. 2 2

Mamy zatem

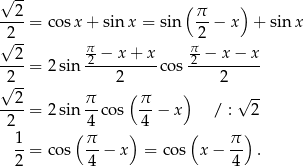
√ 2- (π ) ----= cosx + sin x = sin -- − x + sin x √2-- 2 --2- π2-−-x-+-x- π2 −-x−--x 2 = 2sin 2 co s 2 √ -- ( ) √ -- --2-= 2sin π-cos π- − x / : 2 2 4 4 1 ( π ) ( π ) 2-= cos 4-− x = cos x− 4- .

Podobnie jak w poprzednim sposobie, musimy trochę uważać, bo wprawdzie 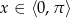x ∈ ⟨0 ,π⟩ , ale

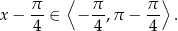
⟨ ⟩ π- π- π- x− 4 ∈ − 4,π − 4 .

Mamy zatem

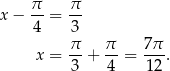
π- π- x − 4 = 3 π π 7π x = --+ --= ---. 3 4 12

Wyjściowe równanie ma więc dwa rozwiązania

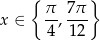
{ π 7π } x ∈ --,--- 4 1 2

 
Odpowiedź: { } x ∈ π4, 7π12-

Wersja PDF