/Szkoła średnia/Równania/Trygonometryczne/Stopnia 1

Zadanie nr 7701377

Rozwiąż równanie 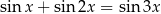sinx + sin 2x = sin 3x w przedziale ⟨0,2π⟩ .

Wersja PDF

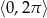Rozwiązanie

Sposób I

Korzystamy ze wzoru

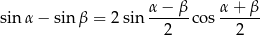
α − β α + β sinα − sin β = 2 sin ------co s------ 2 2

na różnicę sinusów oraz ze wzoru

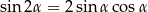
sin 2α = 2sin αco sα

na 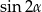sin 2α . Dane równanie możemy więc zapisać w postaci

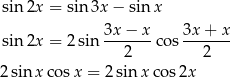
sin 2x = sin 3x− sin x sin 2x = 2 sin 3x-−--xco s 3x-+-x 2 2 2sin xco sx = 2sinx cos 2x

Jeżeli 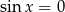sin x = 0 , to w danym przedziale

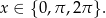
x ∈ {0,π ,2π }.

Jeżeli natomiast 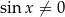sin x ⁄= 0 , to możemy równanie podzielić stronami przez 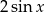2 sin x i mamy

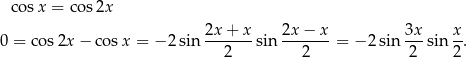
co sx = co s2x 2x-+-x- 2x−--x- 3x- x- 0 = cos 2x − cos x = − 2sin 2 sin 2 = − 2 sin 2 sin 2 .

Jeżeli 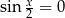x sin 2 = 0 , to automatycznie 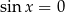sinx = 0 (ze wzoru na 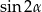sin 2α ), więc w tym przypadku nie otrzymamy żadnych nowych rozwiązań. Jeżeli natomiast 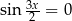sin 3x2 = 0 , to

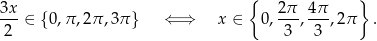
{ } 3x-∈ {0,π ,2π,3π } ⇐ ⇒ x ∈ 0, 2π-, 4π-,2π . 2 3 3

W sumie dane równanie ma więc 5 rozwiązań:

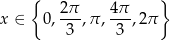
{ } x ∈ 0, 2-π,π , 4π-,2π 3 3

Sposób II

Korzystamy ze wzorów na sumę sinusów i na 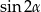sin 2α .

sin 2x + sinx = sin 3x 2 sin 2x-+-x-co s 2x-−-x-= sin3x 2 2 3x x 3x 3x 2 sin ---co s--= 2sin ---cos --- 2 ( 2 2 ) 2 2 sin 3x- cos x-− cos 3x- = 0. 2 2 2

Jeżeli 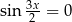sin 32x= 0 to mamy

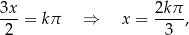
3x-= kπ ⇒ x = 2k-π , 2 3

co danym przedziale prowadzi do rozwiązań

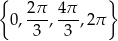
{ } 0, 2π-, 4π-,2π 3 3

Teraz zajmujemy się wyrażeniem w nawiasie.

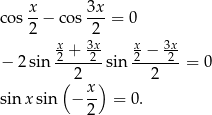
cos x-− cos 3x-= 0 2 2 x + 3x- x − 3x − 2 sin 2----2-sin 2----2-= 0 ( 2 ) 2 sin x sin − x- = 0. 2

Powinno być jasne, że wystarczy zająć się warunkiem 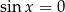sin x = 0 , bo warunek 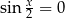sin x2 = 0 i tak implikuje 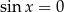sinx = 0 (np. ze wzoru na 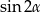sin 2α ). Zatem 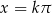x = kπ , czyli w danym przedziale otrzymujemy jedno dodatkowe rozwiązanie: x = π .  
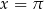Odpowiedź: { } 0, 2π3-,π, 4π3-,2π

Wersja PDF