Zadanie nr 8727615
Rozwiąż równanie 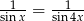 w przedziale
w przedziale 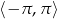 .
.
Rozwiązanie
Na początku zauważmy, że mianowniki muszą być niezerowe, czyli 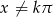 i
i 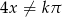 . Po uwzględnieniu podanej dziedziny daje to nam
. Po uwzględnieniu podanej dziedziny daje to nam 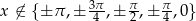 .
.
Sposób I
Korzystamy ze wzoru na różnicę sinusów
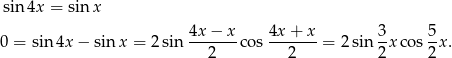
Zatem
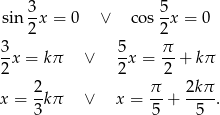
Uwzględniając ograniczenie 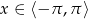 oraz dziedzinę równania daje to nam rozwiązania
oraz dziedzinę równania daje to nam rozwiązania
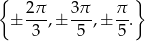
Sposób II
Korzystamy z następującej równoważności
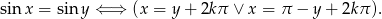
Korzystając z powyższego warunku mamy
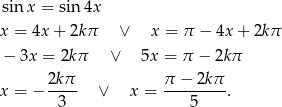
Podobnie jak w poprzednim sposobie, po uwzględnieniu warunku 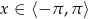 oraz dziedziny otrzymujemy rozwiązania
oraz dziedziny otrzymujemy rozwiązania
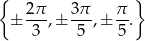
Sposób III
Przekształcimy podane równanie korzystając ze wzoru 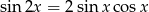 .
.
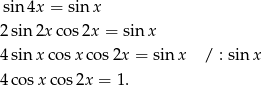
Teraz skorzystamy ze wzoru 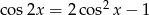 , co sprawi, że w równaniu będzie występował tylko
, co sprawi, że w równaniu będzie występował tylko 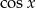 (w różnych potęgach) i będziemy mogli podstawić
(w różnych potęgach) i będziemy mogli podstawić 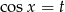 .
.
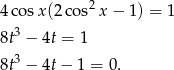
Aby rozwiązać to równanie wielomianowe szukamy jego pierwiastków wymiernych w postaci 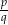 , gdzie
, gdzie 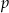 dzieli -1, a
dzieli -1, a 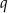 dzieli 8. Łatwo zauważyć, że
dzieli 8. Łatwo zauważyć, że 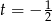 jest takim pierwiastkiem. Dzielimy teraz wielomian przez dwumian
jest takim pierwiastkiem. Dzielimy teraz wielomian przez dwumian 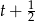 , albo jeszcze lepiej (żeby nie mieć ułamków) przez
, albo jeszcze lepiej (żeby nie mieć ułamków) przez 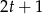 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
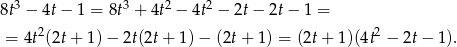
Szukamy teraz miejsc zerowych otrzymanego trójmianu.
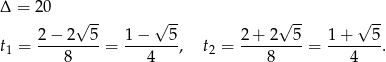
Zatem 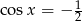 ,
, 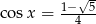 lub
lub 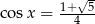 . Pierwszy z tych warunków daje
. Pierwszy z tych warunków daje 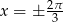 , szkicując sobie wykres cosinusa na przedziale
, szkicując sobie wykres cosinusa na przedziale 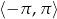 , widać, że każdy z dwóch pozostałych warunków również daje dwa kąty (można je odczytać z tablic - tak się składa, że są to dokładnie kąty
, widać, że każdy z dwóch pozostałych warunków również daje dwa kąty (można je odczytać z tablic - tak się składa, że są to dokładnie kąty 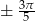 i
i 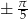 , ale patrząc tylko na tablice nie możemy być tego pewni).
, ale patrząc tylko na tablice nie możemy być tego pewni).
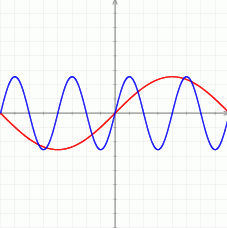
Na koniec, dla ciekawskich, wykresy 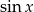 i
i  (szukaliśmy punktów wspólnych tych wykresów).
(szukaliśmy punktów wspólnych tych wykresów).
Odpowiedź: 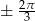 ,
, 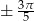 i
i