Zadanie nr 6067427

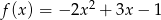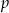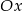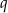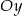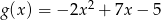Wykres funkcji kwadratowej 2 f(x) = − 2x + 3x− 1 przesunięto o jednostek wzdłuż osi i o jednostek wzdłuż osi . Otrzymano w ten sposób wykres funkcji g(x) = − 2x 2 + 7x − 5 .

Wyznacz liczby 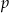i .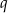
Rozwiąż równanie .

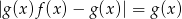Rozwiązanie

Sposób I

Ze wzoru na przesunięcie wykresu funkcji o wektor mamy równanie

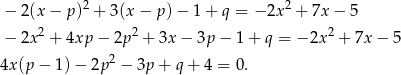
$2 2 − 2(x − p) + 3(x − p )− 1 + q = − 2x + 7x − 5 − 2x2 + 4xp − 2p2 + 3x − 3p − 1 + q = −2x 2 + 7x− 5 4x (p− 1)− 2p2 − 3p + q + 4 = 0.$

Równość ta ma być spełniona dla dowolnego 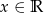, czyli oba współczynniki funkcji liniowej z lewej strony muszą być równe 0. Mamy zatem 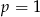oraz

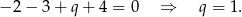
$− 2− 3+ q+ 4 = 0 ⇒ q = 1.$

Sposób II

Wykres funkcji 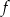ma wierzchołek w punkcie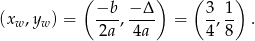

$( ) ( ) (xw ,yw) = −b--, −-Δ = 3-, 1 . 2a 4a 4 8$

Natomiast wierzchołek funkcji 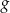ma współrzędne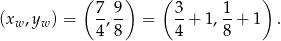

$( 7 9) ( 3 1 ) (xw ,yw) = -,-- = --+ 1,--+ 1 . 4 8 4 8$

Zatem .

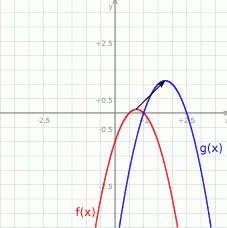
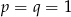Odpowiedź: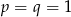
Liczymy
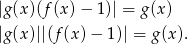
$|g (x)(f(x) − 1)| = g(x ) |g (x)||(f(x )− 1 )| = g(x).$

Zauważmy, że jeżeli 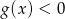to po skróceniu 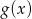dostajemy równanie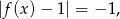

$|f(x) − 1| = − 1,$

które na pewno jest sprzeczne. Zatem musi być 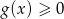. Sprawdźmy kiedy tak jest.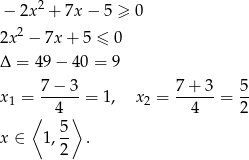

$− 2x 2 + 7x − 5 ≥ 0 2 2x − 7x+ 5 ≤ 0 Δ = 49 − 40 = 9 x = 7-−-3-= 1, x = 7+-3-= 5- 1 ⟨ 4 ⟩ 2 4 2 5 x ∈ 1 ,2- .$

Na końcach przedziału mamy 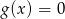, więc są to na pewno rozwiązania równania. Załóżmy dalej, że 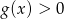, czyli 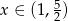. Skracając równanie przez 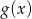mamy

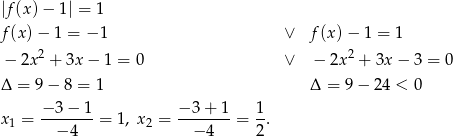
$|f (x)− 1| = 1 f(x) − 1 = − 1 ∨ f(x) − 1 = 1 2 2 − 2x + 3x− 1 = 0 ∨ − 2x + 3x − 3 = 0 Δ = 9 − 8 = 1 Δ = 9− 24 < 0 − 3 − 1 − 3+ 1 1 x1 = ------- = 1, x 2 =------- = -. − 4 − 4 2$

Żadne z tych rozwiązań nie jest w przedziale 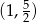, więc jedyne rozwiązania równania to miejsca zerowe .
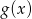Odpowiedź: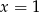 lub