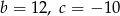/Szkoła średnia/Funkcje - wykresy/Parabola/Przesunięcie wykresu

Zadanie nr 6224906

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykres funkcji 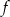f danej wzorem 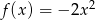2 f(x) = −2x przesunięto wzdłuż osi 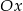Ox o 3 jednostki w prawo oraz wzdłuż osi 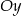Oy o 8 jednostek w górę, otrzymując wykres funkcji g .

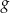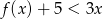  • Rozwiąż nierówność f(x) + 5 < 3x .
  • Podaj zbiór wartości funkcji g .
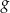  • Funkcja 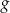g określona jest wzorem 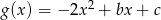g(x) = −2x 2 + bx+ c . Oblicz 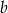b i c .

Rozwiązanie

  • Liczymy
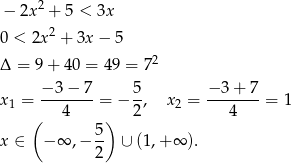
    − 2x 2 + 5 < 3x 2 0 < 2x + 3x − 5 Δ = 9 + 40 = 49 = 72 x = −-3-−-7 = − 5, x = −-3+--7 = 1 1 ( 4 ) 2 2 4 5 x ∈ −∞ ,− -- ∪ (1,+ ∞ ). 2

     
    Odpowiedź: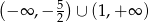 ( ) − ∞ ,− 5 ∪ (1 ,+ ∞ ) 2

  • Najłatwiej jest narysować wykres funkcji 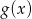g(x) (przesuwamy wykres funkcji 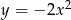y = − 2x 2 zgodnie z opisem).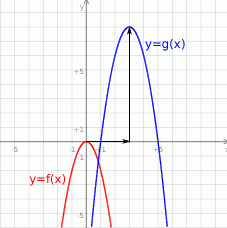
    PIC

    Z wykresu widać, że zbiór wartości jest przedziałem (− ∞ ,8⟩ .  
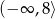    Odpowiedź: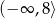 (− ∞ ,8⟩

  • Przesuwając funkcję 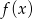f(x ) o 3 jednostki w prawo otrzymujemy funkcję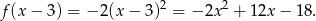
    f(x − 3) = −2 (x− 3)2 = − 2x2 + 12x − 18 .

    Tę funkcję przesuwamy jeszcze o 8 jednostek do góry i mamy

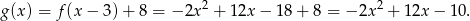
    g (x) = f(x − 3 )+ 8 = − 2x2 + 12x − 18 + 8 = − 2x 2 + 12x − 10.

    Zatem 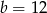b = 12 i c = − 10 .  
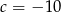    Odpowiedź: b = 12, c = − 10

Wersja PDF