/Szkoła średnia/Funkcje - wykresy/Parabola/Przesunięcie wykresu

Zadanie nr 7154343

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykres funkcji kwadratowej 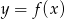y = f (x) przesunięto o 2 jednostki do góry, następnie nowy wykres o 3 jednostki w lewo i otrzymano wykres funkcji 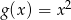g (x ) = x2 . Wyznacz wzór ogólny funkcji f .

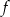Rozwiązanie

Sposób I

Myślimy od końca: wykres funkcji 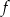f powstaje z wykresu funkcji 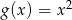g(x) = x2 przez przesunięcie o 3 jednostki w prawo, a potem o 2 jednostki w dół.

PIC

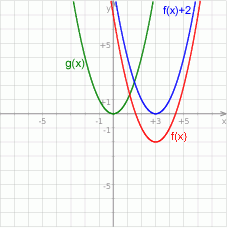
Funkcja 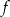f ma więc wzór

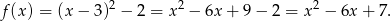
2 2 2 f (x) = (x − 3) − 2 = x − 6x + 9 − 2 = x − 6x + 7.

Sposób II

Szukamy funkcji 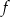f w postaci:

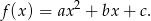
2 f(x) = ax + bx+ c.

Liczymy

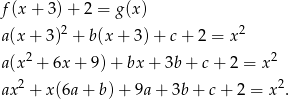
f (x+ 3)+ 2 = g(x) a(x + 3 )2 + b(x + 3 )+ c + 2 = x2 2 2 a(x + 6x + 9)+ bx+ 3b+ c+ 2 = x ax 2 + x (6a+ b)+ 9a+ 3b+ c+ 2 = x2.

Porównujemy współczynniki przy odpowiadających sobie potęgach po obu stronach równania i otrzymujemy

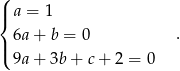
( |{ a = 1 6a+ b = 0 . |( 9a+ 3b + c+ 2 = 0

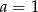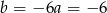Podstawiamy a = 1 i b = − 6a = − 6 w trzecim równaniu Natomiast z trzeciego

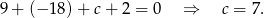
9+ (− 18)+ c+ 2 = 0 ⇒ c = 7.

Zatem ostatecznie otrzymujemy wzór

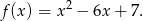
f(x ) = x2 − 6x + 7.

 
Odpowiedź: f (x) = x2 − 6x + 7

Wersja PDF