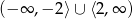/Szkoła średnia/Funkcje - wykresy/Parabola/Przesunięcie wykresu

Zadanie nr 7715998

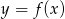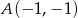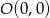Do wykresu funkcji kwadratowej y = f(x) należą punkty A (− 1,− 1) oraz O (0,0) , który jest wierzchołkiem paraboli.

PIC

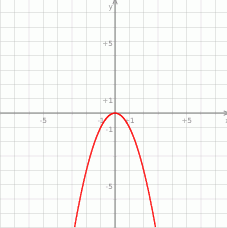
Wykres ten przesunięto w taki sposób, że otrzymano wykres funkcji 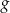g , której miejscami zerowymi są liczby 3 i 7.

  • Oblicz współrzędne wierzchołka paraboli będącej wykresem funkcji g .
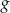  • Narysuj wykres funkcji y = g (x) .
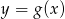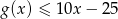  • Rozwiąż nierówność g(x) ≤ 1 0x− 25 .
Wersja PDF

Rozwiązanie

  • Z podanych informacji wynika, że 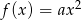f(x) = ax 2 (bo 0 jest podwójnym pierwiastkiem), ponadto 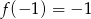f(− 1) = −1 , co daje 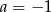a = − 1 . Przesunięta funkcja będzie miała taki sam współczynnik przy 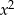x2 , ma więc wzór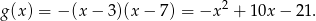
    2 g(x) = − (x− 3)(x− 7) = −x + 10x − 21 .

    Wierzchołek tej paraboli to punkt

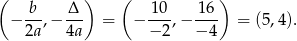
    ( b Δ ) ( 10 16) − --,− --- = − ---,− ---- = (5,4 ). 2a 4a − 2 − 4

     
    Odpowiedź: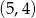 (5,4)

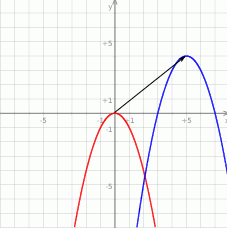
  • Rysujemy go bez trudu, korzystając z poprzedniego podpunktu.
    PIC
  • Do rozwiązania mamy nierówność
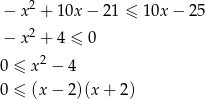
    − x 2 + 10x − 21 ≤ 10x − 2 5 2 − x + 4 ≤ 0 0 ≤ x2 − 4 0 ≤ (x− 2)(x + 2)

    Rozwiązaniem tej nierówności jest zbiór 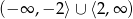(− ∞ ,− 2⟩∪ ⟨2,∞ ) (oba składniki muszą być niedodatnie lub nieujemne).  
    Odpowiedź: (− ∞ ,− 2⟩∪ ⟨2,∞ )

Wersja PDF