/Szkoła średnia/Funkcje - wykresy/Logarytmy/Rysowanie wykresu

Zadanie nr 6231792

Narysuj wykres funkcji 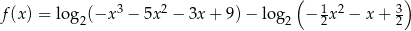3 2 ( 1 2 3) f (x) = log2(−x − 5x − 3x + 9 )− log2 − 2x − x + 2 .

Wersja PDF

Rozwiązanie

Rozpocznijmy od rozłożenia wielomianów, które są logarytmowane na czynniki. Łatwo zauważyć, że pierwiastkiem pierwszego z nich jest np. 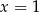x = 1 . Dzielimy więc go przez dwumian (x − 1) .

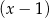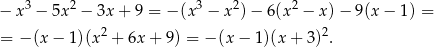
− x3 − 5x2 − 3x + 9 = − (x3 − x2) − 6(x 2 − x )− 9(x − 1 ) = 2 2 = − (x − 1)(x + 6x + 9) = −(x − 1 )(x+ 3) .

Wyrażenie to jest dodatnie dla

x ∈ (− ∞ ,− 3)∪ (− 3,1 ).

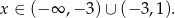
Rozkładamy teraz drugi wielomian

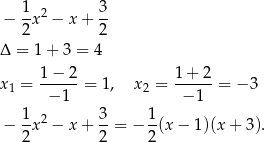
1-2 3- − 2x − x + 2 Δ = 1 + 3 = 4 1-−-2- 1+--2- x1 = − 1 = 1, x2 = − 1 = − 3 1 3 1 − -x2 − x + --= − -(x − 1 )(x+ 3). 2 2 2

To wyrażenie jest dodatnie dla 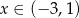x ∈ (− 3,1 ) . Dziedziną funkcji 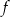f jest więc przedział (− 3,1) .

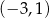Przekształcamy teraz wzór funkcji

[ ] [ 1 ] f(x ) = lo g2 − (x − 1)(x + 3 )2 − log 2 − --(x− 1)(x + 3) = 2 − (x− 1)(x+ 3)2 = lo g2---1-------------- = log 22(x + 3) = − 2(x− 1)(x + 3) = lo g 2 + log (x + 3) = 1+ lo g (x+ 3). 2 2 2

Widać teraz, że wykres funkcji 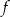f powstaje z wykresu funkcji 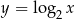y = lo g2x przez przesunięcie o 3 jednostki w lewo i 1 jednostkę do góry. Pozostało naszkicować wykres.

PIC

Wersja PDF