/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy trójkątny

Zadanie nr 3541104

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość 6. Oblicz objętość tego ostrosłupa jeżeli kąt nachylenia krawędzi bocznej do podstawy ma miarę 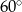60∘ .

Rozwiązanie

Zaczynamy od schematycznego rysunku.

PIC

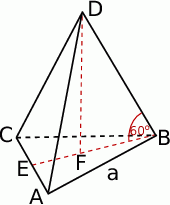
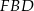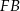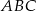Wysokość ostrosłupa wyliczymy z trójkąta prostokątnego FBD , najpierw musimy jednak wyliczyć długość odcinka F B . Jest równy 23 wysokości trójkąta ABC (tak środek trójkąta równobocznego dzieli wysokość).

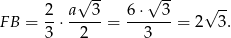
-- -- 2 a√ 3 6⋅√ 3 √ -- F B = --⋅ -----= ------= 2 3. 3 2 3

Mamy zatem

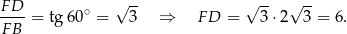
F D ∘ √ -- √ -- √ -- ---- = tg6 0 = 3 ⇒ F D = 3⋅ 2 3 = 6. FB

Liczymy teraz objętość (korzystamy ze wzoru na pole trójkąta równobocznego).

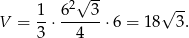
√ -- 1 6 2 3 √ -- V = --⋅------⋅ 6 = 18 3. 3 4

 
Odpowiedź: √ -- 18 3

Wersja PDF