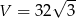Zadanie nr 5245502
Podstawą ostrosłupa prawidłowego jest trójkąt równoboczny. Wysokość ściany bocznej tego ostrosłupa jest równa 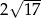 , a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy 4. Oblicz objętość tego ostrosłupa.
, a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy 4. Oblicz objętość tego ostrosłupa.
Rozwiązanie
Dorysujmy wysokość ściany bocznej.
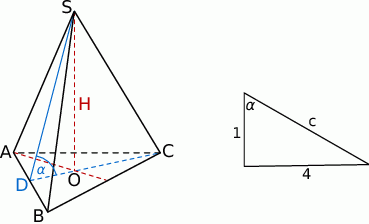
Sposób I
Jeżeli oznaczymy wysokość ostrosłupa przez 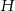 , to z podanego tangensa kąta
, to z podanego tangensa kąta  nachylenia ściany bocznej do podstawy mamy
nachylenia ściany bocznej do podstawy mamy
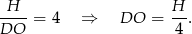
Piszemy teraz twierdzenie Pitagorasa w trójkącie 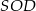 .
.
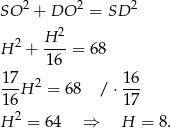
Stąd 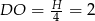 . Jeżeli oznaczymy przez
. Jeżeli oznaczymy przez  długość krawędzi podstawy ostrosłupa, to mamy
długość krawędzi podstawy ostrosłupa, to mamy
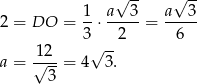
Liczymy teraz objętość ostrosłupa.
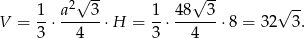
Sposób II
Tym razem obliczmy najpierw 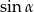 i
i 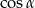 . Szkicujemy trójkąt prostokątny, w którym
. Szkicujemy trójkąt prostokątny, w którym 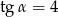 . Z twierdzenia Pitagorasa obliczamy długość przeciwprostokątnej tego trójkąta.
. Z twierdzenia Pitagorasa obliczamy długość przeciwprostokątnej tego trójkąta.
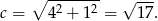
Stąd
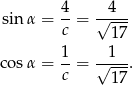
Teraz z trójkąta prostokątnego 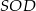 obliczamy długości odcinka
obliczamy długości odcinka 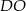 i wysokości ostrosłupa.
i wysokości ostrosłupa.
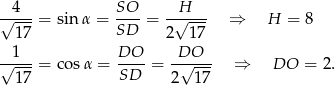
Długość krawędzi podstawy i objętość obliczamy tak samo jak w poprzednim sposobie.
Odpowiedź: