/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy trójkątny

Zadanie nr 6061498

Krawędź podstawy ostrosłupa trójkątnego prawidłowego jest równa 6. Jego objętość jest równa 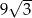√ -- 9 3 . Wyznacz długość wysokości ściany bocznej ostrosłupa.

Wersja PDF

Rozwiązanie

Rozpoczynamy od szkicowego rysunku

PIC

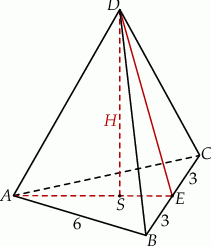
Z podanej objętości łatwo jest wyliczyć długość wysokości ostrosłupa (korzystamy ze wzoru 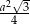√ - a2-3 4 na pole trójkąta równobocznego).

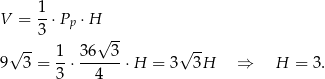
1- V = 3 ⋅Pp ⋅H √ -- √ -- √ -- 9 3 = 1-⋅ 36--3-⋅H = 3 3H ⇒ H = 3. 3 4

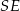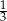Długość odcinka SE to 1 3 wysokości trójkąta równobocznego 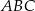ABC , czyli

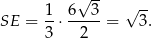
√ -- 1- 6--3- √ -- SE = 3 ⋅ 2 = 3.

Pozostało teraz zastosować twierdzenie Pitagorasa w trójkącie prostokątnym SED .

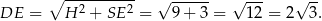
∘ ---------- ------ √ --- -- DE = H 2 + SE 2 = √ 9 + 3 = 12 = 2√ 3 .

 
Odpowiedź: √ -- 2 3

Wersja PDF