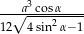/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy trójkątny

Zadanie nr 6150522

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość a . Ściany boczne są trójkątami ostrokątnymi. Miara kąta między sąsiednimi ścianami bocznymi jest równa 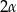2 α . Wyznacz objętość tego ostrosłupa.

Rozwiązanie

Musimy najpierw ustalić jak wyliczyć kąt między ścianami bocznymi.

PIC

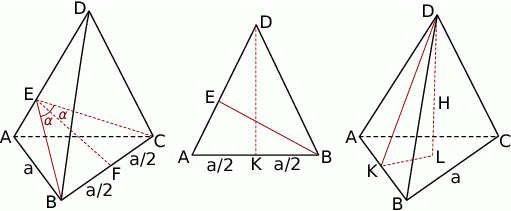
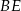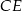Ogólnie, taki kąt wyznacza się przecinając kąt dwuścienny płaszczyzną prostopadłą do krawędzi kąta i liczy się miarę otrzymanego kąta płaskiego. W naszej sytuacji sprawa jest dość prosta. Jeżeli poprowadzimy wysokości BE i CE w trójkątach ścian bocznych, opuszczone na krawędź 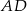AD , to ponieważ ostrosłup jest prawidłowy (ściany są przystające), to spodki tych wysokości będą dokładnie w tym samym punkcie, oznaczmy go przez 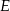E . Otrzymana płaszczyzna jest prostopadła do krawędzi 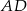AD , zatem kąt 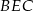BEC jest kątem między ścianami bocznymi.

Sposób I

Z trójkąta prostokątnego 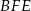BF E mamy

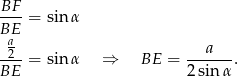
BF- = sin α BE a2 a --- = sin α ⇒ BE = -------. BE 2 sinα

Teraz patrzymy na trójkąt prostokątny 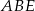ABE

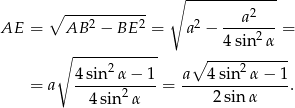
∘ ------------- ∘ ------------ 2 AE = AB 2 − BE 2 = a2 − ---a----= 4 sin 2α ∘ ------------ ∘ ------------ 4-sin2-α-−-1- a--4-sin-2α-−-1- = a 2 = 2sin α . 4sin α

Teraz patrzymy na trójkąty podobne 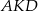AKD i AEB .

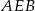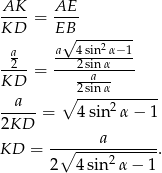
AK--= AE-- KD EB√ -------- a a 4sin2α−1 -2-- ---2-sinα--- KD = --a-- a ∘ 2-sinα------- ----- = 4 sin2α − 1 2KD KD = -∘----a--------. 2 4 sin 2α − 1

Teraz patrzymy na trójkąt prostokątny 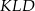KLD – wyliczamy z niego wysokość ostrosłupa.

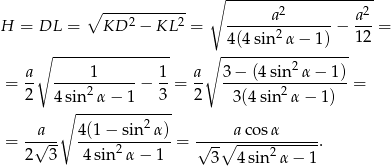
∘ --------------------- ∘ ------------ 2 2 H = DL = KD 2 − KL 2 = ------a--------− a--= 4(4 sin2α − 1) 12 ∘ ---------------- ∘ ------------------ a- -----1------ 1- a- 3−--(4sin2α-−-1-) = 2 4sin2α − 1 − 3 = 2 3(4 sin 2α − 1) = ∘ -------------- a 4(1− sin 2α) a cosα = -√--- -----2-------= √--∘-------------. 2 3 4sin α − 1 3 4sin2α − 1

Teraz bez trudu liczymy objętość

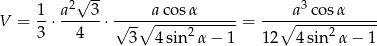
√ -- 1- a-2--3 -----aco-sα------ ----a3-cosα----- V = 3 ⋅ 4 ⋅ √ -∘ -----2------= ∘ ----2------- 3 4 sin α − 1 12 4sin α − 1

Sposób II

Z trójkąta 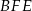BF E mamy

BF BF a --- = tg α ⇒ EF = ----= -----. EF tg α 2tg α

Dokładnie tak samo jak w poprzednim sposobie wyliczamy

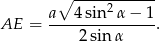
∘ -----2------ AE = a--4-sin--α-−-1. 2sin α

Tym razem jednak nie będziemy liczyć wysokości ściany bocznej, ale od razu wyliczymy wysokość ostrosłupa. Patrzymy na trójkąt 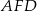AF D .

PIC

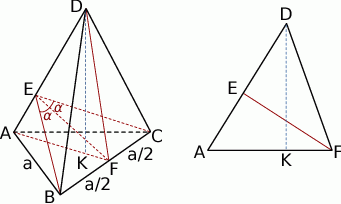
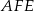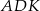Trójkąty AF E i ADK są podobne (oba są prostokątne i mają wspólny kąt 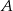A ). Mamy więc

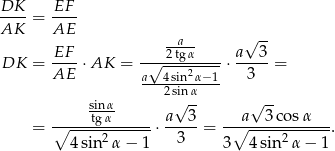
DK EF AK-- = AE-- -a-- √ -- -EF- -√--2tgα--- a---3 DK = AE ⋅AK = a 4 sin2α−1 ⋅ 3 = ---2sinα---- sinα √ -- √ -- = ∘-----tgα------⋅ a--3-= -∘a--3-cosα---. 4sin2α − 1 3 3 4 sin 2α − 1

Pozostało policzyć objętość ostrosłupa.

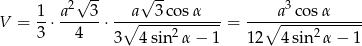
√ -- √ -- 1 a 2 3 a 3 cos α a3 cosα V = --⋅------⋅ -∘------2------= --∘------2------- 3 4 3 4 sin α − 1 12 4sin α − 1

 
Odpowiedź: 3 --√a-cos2α--- 12 4sin α− 1

Wersja PDF