Zadanie nr 1867410
Wykaż, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność:
prawdziwa jest nierówność:
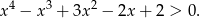
Rozwiązanie
Sposób I
Zauważmy, że
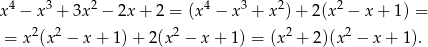
Oczywiście wyrażenie w pierwszym nawiasie jest dodatnie. Wyrażenie w drugim nawiasie też jest dodatnie, bo
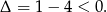
Sposób II
Próbujemy zapisać lewą stronę nierówności jako sumę wyrażeń, które są nieujemne – spróbujemy pozbyć się minusów wciągając je do wyrażeń postaci 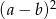 .
.
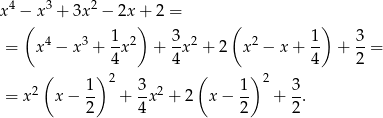
Teraz jest jasne, że wyrażenie to jest dodatnie. Co więcej, widać, że prawdziwa jest mocniejsza nierówność
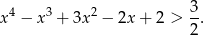
Sposób III
Tym razem użyjemy pochodnych. Jeżeli 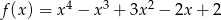 to
to
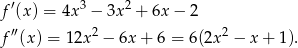
Zauważmy, że druga pochodna jest stale dodatnia (bo 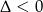 ), więc pierwsza pochodna jest funkcją rosnącą. Pierwsza pochodna jako wielomian stopnia 3 ma więc dokładnie jeden pierwiastek
), więc pierwsza pochodna jest funkcją rosnącą. Pierwsza pochodna jako wielomian stopnia 3 ma więc dokładnie jeden pierwiastek 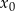 i zmienia w nim znak z ujemnego na dodatni. To oznacza, że funkcja
i zmienia w nim znak z ujemnego na dodatni. To oznacza, że funkcja 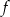 ma jedno minimum lokalne w
ma jedno minimum lokalne w 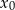 , które jednocześnie jest minimum globalnym (bo na lewo od
, które jednocześnie jest minimum globalnym (bo na lewo od 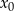 funkcja
funkcja 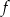 maleje, a na prawo rośnie).
maleje, a na prawo rośnie).
Spróbujmy teraz oszacować, ile jest równe 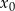 . Zauważmy, że
. Zauważmy, że
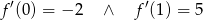
Zatem 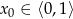 . To nam trochę upraszcza sprawę, bo wiemy, że funkcja
. To nam trochę upraszcza sprawę, bo wiemy, że funkcja 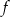 najmniejszą wartość przyjmuje w przedziale
najmniejszą wartość przyjmuje w przedziale 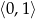 . Wystarczy zatem pokazać, że
. Wystarczy zatem pokazać, że 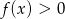 dla
dla 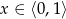 . Zauważmy, że
. Zauważmy, że
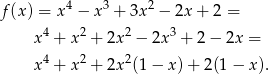
Widać teraz, że wyrażenie to jest dodatnie na przedziale 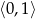 .
.
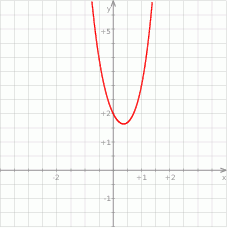
Na koniec wykres funkcji 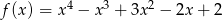 .
.