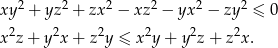Zadanie nr 2209237
Udowodnij, że dla dowolnych liczb rzeczywistych 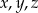 takich, że
takich, że 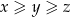 , prawdziwa jest nierówność
, prawdziwa jest nierówność
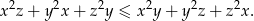
Możesz skorzystać z tożsamości
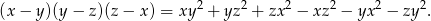
Rozwiązanie
Zauważmy, że na mocy danego założenia 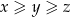 mamy
mamy
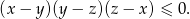
Zatem z danej tożsamości mamy
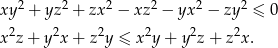
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Udowodnij, że dla dowolnych liczb rzeczywistych 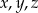 takich, że
takich, że 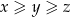 , prawdziwa jest nierówność
, prawdziwa jest nierówność
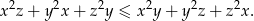
Możesz skorzystać z tożsamości
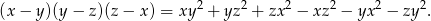
Zauważmy, że na mocy danego założenia 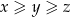 mamy
mamy
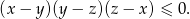
Zatem z danej tożsamości mamy