/Szkoła średnia/Nierówności/Udowodnij.../Wielomianowe

Zadanie nr 3168582

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest wielomian 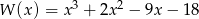3 2 W (x) = x + 2x − 9x − 18 .

  • Wyznacz pierwiastki tego wielomianu.
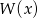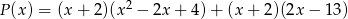  • Sprawdź, czy wielomiany W (x ) i P(x ) = (x+ 2)(x2 − 2x + 4) + (x + 2)(2x − 1 3) są równe.
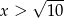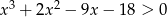  • Uzasadnij, że jeśli √ --- x > 10 , to 3 2 x + 2x − 9x − 18 > 0 .

Rozwiązanie

  • Żeby znaleźć pierwiastki, wstawiamy do wielomianu dzielniki wyrazu wolnego, czyli liczby 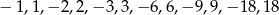− 1,1,− 2,2,− 3,3,− 6,6,− 9,9,− 18 ,18 tak długo aż dla jakiejś wyjdzie 0 – wychodzi już dla 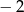− 2 . Jak już mamy pierwiastek, to dzielimy wielomian przez 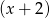(x+ 2) . Robimy to tak jak umiemy, schemat Hornera, dzielenie wielomianów lub grupowanie odpowiednich czynników. My zrobimy to tą ostatnią metodą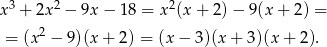
    x3 + 2x 2 − 9x − 1 8 = x2(x + 2) − 9(x + 2) = = (x 2 − 9)(x + 2 ) = (x− 3)(x + 3)(x + 2).

    Teraz widzimy, że pierwiastki to − 2,− 3,3 .  
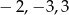    Odpowiedź: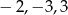 − 2,− 3,3

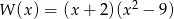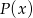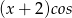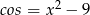  • Z poprzedniego podpunktu wiemy, że W (x) = (x+ 2)(x2 − 9) . Zapiszemy teraz P (x) w postaci (x + 2)cos i sprawdzimy czy 2 cos = x − 9 .
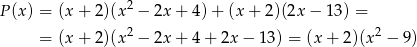
    2 P(x ) = (x + 2)(x − 2x + 4) + (x + 2)(2x − 13) = = (x + 2)(x2 − 2x + 4 + 2x − 1 3) = (x + 2)(x2 − 9)

    i wyszło to samo, czyli są równe. Oczywiście zamiast wyłączać 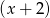(x + 2) przed nawias mogliśmy wszystko powymnażać, ale rachunki byłyby znacznie gorsze.  
    Odpowiedź: Tak, są równe.

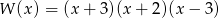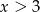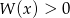  • Ponieważ W (x) = (x + 3)(x + 2 )(x − 3) , to dla x > 3 mamy W (x) > 0 (bo każdy z czynników 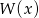W (x) jest dodatni). Teraz wystarczy zauważyć, że √ --- √ -- 10 > 9 = 3 .

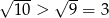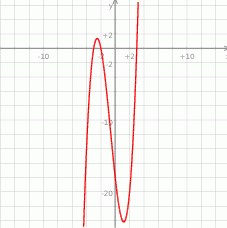
Na koniec, dla ciekawskich, wykres funkcji 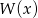W (x) .

PIC
Wersja PDF