Zadanie nr 5157643
Udowodnij, że dla dowolnych różnych liczb rzeczywistych 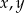 prawdziwa jest nierówność
prawdziwa jest nierówność
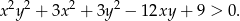
Rozwiązanie
Sposób I
Przekształcamy daną nierówność w sposób równoważny.
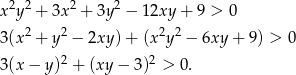
Otrzymana nierówność jest oczywiście spełniona (bo z założenia 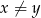 ), a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musiała być spełniona.
), a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musiała być spełniona.
Sposób II
Traktujemy lewą stronę nierówności jak funkcję kwadratową
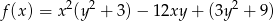
zmiennej  z parametrem
z parametrem 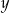 . Ponieważ
. Ponieważ
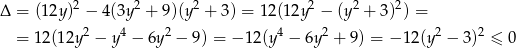
parabola będąca wykresem funkcji 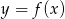 nigdy nie ma punktów leżących poniżej osi
nigdy nie ma punktów leżących poniżej osi 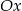 (dla
(dla 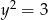 jest styczna do osi
jest styczna do osi 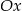 , a w pozostałych przypadkach leży w całości powyżej osi
, a w pozostałych przypadkach leży w całości powyżej osi 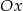 ). To oznacza, że faktycznie zawsze
). To oznacza, że faktycznie zawsze 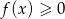 . Aby udowodnić ostrą nierówność zauważmy, że równość może zachodzić tylko gdy
. Aby udowodnić ostrą nierówność zauważmy, że równość może zachodzić tylko gdy 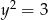 . Wtedy
. Wtedy
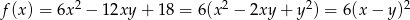
i równość 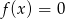 prowadzi do sprzeczności z założeniem
prowadzi do sprzeczności z założeniem 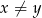 .
.
Sposób III
Przekształcamy daną nierówność w sposób równoważny.
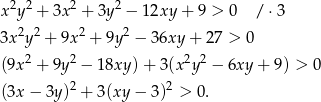
Otrzymana nierówność jest oczywiście spełniona (bo z założenia 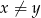 ), a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musiała być spełniona.
), a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musiała być spełniona.
Sposób IV
Przekształcamy daną nierówność w sposób równoważny.
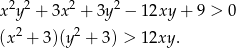
Zauważmy teraz, że na mocy nierówności między średnią arytmetyczną i geometryczną mamy
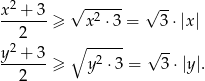
Mamy stąd
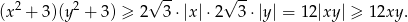
Ponadto równość zachodzi dokładnie wtedy, gdy 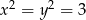 i
i 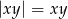 , czyli gdy
, czyli gdy 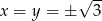 . Ponieważ z założenia
. Ponieważ z założenia 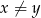 , mamy
, mamy
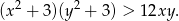
Sposób V
Tak jak w poprzednim sposobie przekształcamy nierówność do postaci
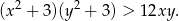
Zauważmy teraz, że jeżeli liczby  i
i 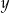 różnią się znakiem, lub gdy jedna z nich jest zerem, to nierówność jest oczywiście spełniona (lewa strona jest zawsze dodatnia). Jeżeli natomiast obie są ujemne, to możemy zmienić znaki obu liczb i nierówność pozostanie dokładnie taka sama (dokładniej: możemy podstawić
różnią się znakiem, lub gdy jedna z nich jest zerem, to nierówność jest oczywiście spełniona (lewa strona jest zawsze dodatnia). Jeżeli natomiast obie są ujemne, to możemy zmienić znaki obu liczb i nierówność pozostanie dokładnie taka sama (dokładniej: możemy podstawić 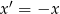 i
i 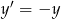 i pozostanie do udowodnienia nierówność z liczbami dodatnimi
i pozostanie do udowodnienia nierówność z liczbami dodatnimi 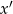 i
i 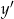 ). Możemy więc założyć, że
). Możemy więc założyć, że 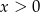 i
i 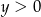 . Dzielimy wtedy nierówność stronami przez
. Dzielimy wtedy nierówność stronami przez 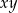 i mamy
i mamy
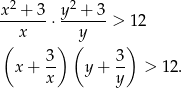
Zauważmy teraz, że
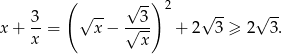
Ponadto równość zachodzi wtedy i tylko wtedy, gdy 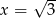 . Analogicznie
. Analogicznie
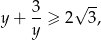
więc
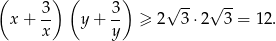
Ponadto równość zachodzi wtedy i tylko wtedy, gdy 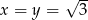 , więc przy założeniu
, więc przy założeniu 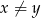 nierówność jest ostra.
nierówność jest ostra.
Sposób VI
Tak samo jak w poprzednim sposobie zauważmy, że możemy założyć, że 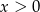 i
i 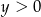 oraz sprowadzamy nierówność do postaci
oraz sprowadzamy nierówność do postaci
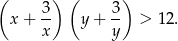
Badamy teraz przebieg zmienności funkcji 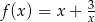 dla
dla 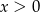 . Liczymy pochodną
. Liczymy pochodną
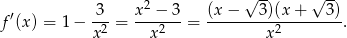
Widać teraz, że pochodna jest ujemna w przedziale 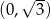 i dodatnia w przedziale
i dodatnia w przedziale 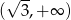 . To oznacza, że w
. To oznacza, że w 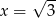 funkcja przyjmuje najmniejszą wartość i mamy
funkcja przyjmuje najmniejszą wartość i mamy
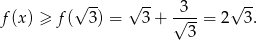
Mamy stąd
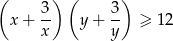
Ponadto równość zachodzi wtedy i tylko wtedy, gdy 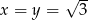 , więc przy założeniu
, więc przy założeniu 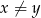 nierówność jest ostra.
nierówność jest ostra.

