/Szkoła średnia/Nierówności/Udowodnij.../Wielomianowe

Zadanie nr 6182048

Udowodnij, że dla każdej liczby rzeczywistej x prawdziwa jest nierówność

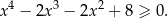
4 3 2 x − 2x − 2x + 8 ≥ 0.
Wersja PDF

Rozwiązanie

Sposób I

Zauważmy, że

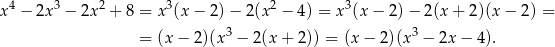
x4 − 2x3 − 2x2 + 8 = x 3(x− 2)− 2(x2 − 4) = x3(x − 2) − 2(x + 2 )(x− 2) = 3 3 = (x − 2)(x − 2(x+ 2)) = (x − 2)(x − 2x − 4 ).

Łatwo teraz sprawdzić, że 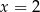x = 2 jest pierwiastkiem wielomianu stopnia 3 w drugim nawiasie. Dzielimy go przez 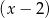(x− 2) – my zrobimy to grupując wyrazy.

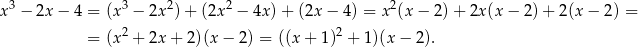
3 3 2 2 2 x − 2x − 4 = (x − 2x )+ (2x − 4x)+ (2x − 4) = x (x − 2)+ 2x (x − 2)+ 2(x − 2) = = (x 2 + 2x + 2)(x− 2) = ((x + 1)2 + 1)(x − 2).

Mamy zatem

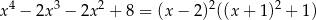
4 3 2 2 2 x − 2x − 2x + 8 = (x− 2) ((x + 1) + 1)

Oczywiście wyrażenie to jest nieujemne.

Sposób II

Tym razem użyjemy pochodnych. Jeżeli 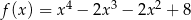4 3 2 f(x) = x − 2x − 2x + 8 to

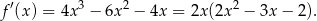
′ 3 2 2 f (x) = 4x − 6x − 4x = 2x (2x − 3x − 2).

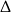Liczymy Δ –ę trójmianu w nawiasie.

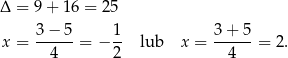
Δ = 9+ 16 = 25 3-−-5- 1- 3+--5- x = 4 = − 2 lub x = 4 = 2.

Zatem

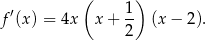
( ) f′(x) = 4x x+ 1- (x − 2 ). 2

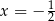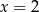To oznacza, że pochodna zmienia znak z ujemnego na dodatni w punktach x = − 1 2 i x = 2 . Zatem w tych punktach funkcja 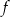f ma minima lokalne i wartość w jednym z tych punktów jest najmniejszą wartością funkcji 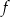f . Liczymy

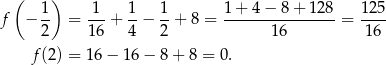
( ) f − 1- = -1-+ 1-− 1-+ 8 = 1-+-4-−-8-+-128-= 125- 2 1 6 4 2 16 16 f(2) = 16 − 16 − 8 + 8 = 0.

W takim razie 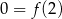0 = f(2) jest najmniejszą wartością funkcji 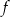f i rzeczywiście

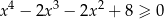
x4 − 2x3 − 2x2 + 8 ≥ 0

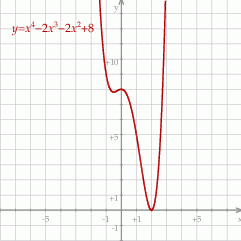
Na koniec wykres funkcji 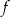f dla ciekawskich.

PIC

Sposób III

Zauważmy, że

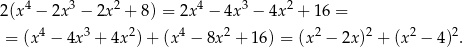
2(x4 − 2x 3 − 2x 2 + 8 ) = 2x4 − 4x3 − 4x 2 + 16 = 4 3 2 4 2 2 2 2 2 = (x − 4x + 4x )+ (x − 8x + 16) = (x − 2x ) + (x − 4) .

Stąd

1 ( ) x4 − 2x 3 − 2x 2 + 8 =-- (x 2 − 2x )2 + (x 2 − 4 )2 ≥ 0. 2
Wersja PDF