Zadanie nr 8586741
Funkcja 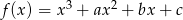 ma trzy różne miejsca zerowe:
ma trzy różne miejsca zerowe: 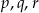 . Wykaż, że
. Wykaż, że
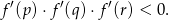
Rozwiązanie
Wiemy, że
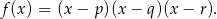
Liczymy pochodną tej funkcji korzystając ze wzoru na pochodną iloczynu
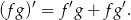
Liczymy
![f ′(x ) = [(x − p )(x− q)(x − r)]′ = ′ ′ = (x− p) ⋅(x − q)(x − r) + (x − p )[(x− q)(x− r)] = = (x− q)(x− r)+ (x− p)(x − r)+ (x− p)(x − q).](https://img.zadania.info/zad/8586741/HzadR2x.gif)
Stąd
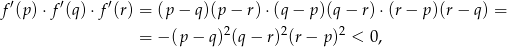
bo wiemy, że pierwiastki są różne.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Funkcja 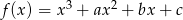 ma trzy różne miejsca zerowe:
ma trzy różne miejsca zerowe: 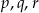 . Wykaż, że
. Wykaż, że
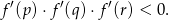
Wiemy, że
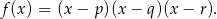
Liczymy pochodną tej funkcji korzystając ze wzoru na pochodną iloczynu
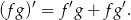
Liczymy
![f ′(x ) = [(x − p )(x− q)(x − r)]′ = ′ ′ = (x− p) ⋅(x − q)(x − r) + (x − p )[(x− q)(x− r)] = = (x− q)(x− r)+ (x− p)(x − r)+ (x− p)(x − q).](https://img.zadania.info/zad/8586741/HzadR2x.gif)
Stąd
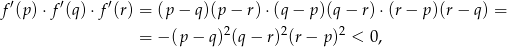
bo wiemy, że pierwiastki są różne.
