Zadanie nr 8909577
Udowodnij, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
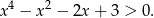
Rozwiązanie
Sposób I
Zauważmy, że
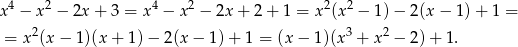
Widać, że 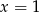 jest wciąż pierwiastkiem wielomianu w drugim nawiasie, więc wielomian ten jest podzielny przez
jest wciąż pierwiastkiem wielomianu w drugim nawiasie, więc wielomian ten jest podzielny przez 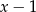 . Dzielimy
. Dzielimy
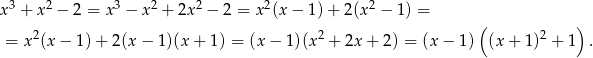
Mamy zatem
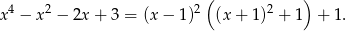
Teraz jest jasne, że wyrażenie to jest zawsze dodatnie, a nawet jest prawdziwa nierówność
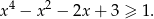
Sposób II
Próbujemy zapisać lewą stronę nierówności jako sumę wyrażeń, które są nieujemne – spróbujemy pozbyć się minusów wciągając je do wyrażeń postaci 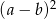 .
.
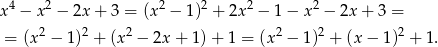
Teraz jest jasne, że wyrażenie to jest zawsze dodatnie, a nawet jest prawdziwa nierówność
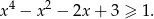
Sposób III
Tym razem użyjemy pochodnych. Jeżeli 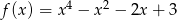 to
to
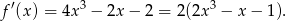
Aby określić znak pochodnej rozłożymy ją na czynniki. Widać, że 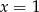 jest pierwiastkiem, więc dzielimy pochodną przez
jest pierwiastkiem, więc dzielimy pochodną przez 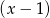 .
.
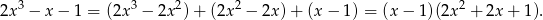
Trójmian w nawiasie jest stale dodatni, bo 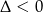 , więc pochodna jest ujemna na przedziale
, więc pochodna jest ujemna na przedziale 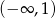 i dodatnia na przedziale
i dodatnia na przedziale 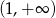 . To oznacza, że punkcie
. To oznacza, że punkcie 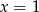 funkcja
funkcja 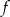 ma minimum lokalne, które jest równe
ma minimum lokalne, które jest równe
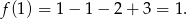
Zatem rzeczywiście
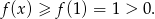
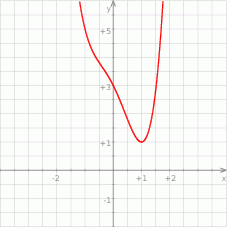
Na koniec obrazek