/Szkoła średnia/Liczby/Działania na liczbach

Zadanie nr 3162823

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że nie istnieje taka liczba rzeczywista x , aby suma tej liczby i jej odwrotności była równa 1.

Rozwiązanie

Oczywiste jest, że liczba taka nie może być równa 0, więc możemy w dalszej części założyć, że 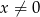x ⁄= 0 .

Zapiszmy równanie

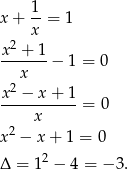
x + -1 = 1 x x 2 + 1 -------− 1 = 0 x x-2 −-x-+-1 x = 0 2 x − x + 1 = 0 Δ = 12 − 4 = − 3.

Zatem równanie jest sprzeczne, czyli nie istnieje liczba rzeczywista taka, że suma jej i jej odwrotności jest równa 1.

Wersja PDF