/Szkoła średnia/Ciągi/Arytmetyczny/Dany przez kolejne wyrazy

Zadanie nr 1575151

Dodaj do ulubionych
Dodaj do rozwiązanych

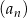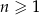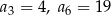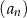W ciągu arytmetycznym (an) , określonym dla n ≥ 1 , dane są wyrazy: a3 = 4 , a6 = 1 9 . Wyznacz wszystkie wartości n , dla których wyrazy ciągu (an) są mniejsze od 200.

Rozwiązanie

Korzystając ze wzoru 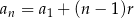an = a1 + (n− 1)r na n –ty wyraz ciągu arytmetycznego otrzymujemy układ równań

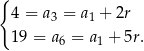
{ 4 = a3 = a1 + 2r 19 = a = a + 5r. 6 1

Odejmując od drugiego równania pierwsze (żeby skrócić 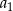a1 ) mamy

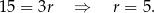
15 = 3r ⇒ r = 5.

Zatem 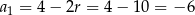a1 = 4 − 2r = 4 − 10 = − 6 oraz

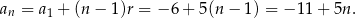
an = a1 + (n− 1)r = − 6 + 5(n − 1) = − 11 + 5n .

Pozostało rozwiązać nierówność

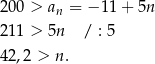
20 0 > a = − 11 + 5n n 21 1 > 5n / : 5 42 ,2 > n.

Zatem wyrazy ciągu o numerach 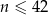n ≤ 42 są mniejsze od 200.  
Odpowiedź: n ≤ 42

Wersja PDF