Zadanie nr 3383838

Trzy początkowe wyrazy malejącego ciągu arytmetycznego są pierwiastkami wielomianu 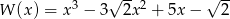√ -- √ -- W (x) = x3 − 3 2x2 + 5x − 2 , a jednym z nich jest √ -- 2 .

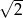Znajdź pierwszy wyraz tego ciągu.
Oblicz sumę .

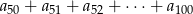Rozwiązanie

Skoro wiemy, że 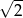jest pierwiastkiem wielomianu 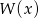, to dzielimy go przez 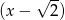. My wykonamy to dzielenie grupując wyrazy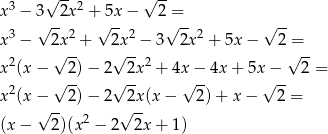
$3 √ -- 2 √ -- x − 3√ -2x +√5x-− 2 =√-- √ -- x3 − 2x 2 + 2x 2 − 3 2x2 + 5x − 2 = √ -- √ -- √ -- x2(x − 2 )− 2 2x2 + 4x − 4x + 5x − 2 = 2 √ -- √ -- √ -- √ -- x (x −√ --2 )− 2 √ 2x(x − 2) + x − 2 = (x − 2)(x 2 − 2 2x + 1)$

Pozostało znaleźć pierwiastki trójmianu kwadratowego w nawiasie. Liczymy 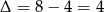, skąd pierwiastki to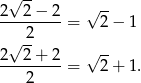

$2√ 2-− 2 √ -- ---------= 2− 1 √ -2 2 2 + 2 √ -- ---------= 2+ 1. 2$

Mamy zatem

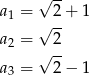
$√ -- a1 = √ 2+ 1 a2 = 2 √ -- a3 = 2− 1$

Odpowiedź: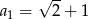
Z poprzedniego podpunktu wiemy, że
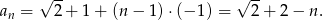
$a = √ 2+ 1+ (n − 1)⋅ (− 1) = √ 2+ 2− n. n$

Szukana suma to suma 51 wyrazów ciągu arytmetycznego o pierwszym wyrazie 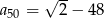i różnicy 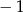. Zatem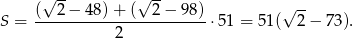

$√ -- √ -- √ -- S = (--2-−-48)-+-(--2-−-98)-⋅51 = 51( 2 − 73). 2$

Mogliśmy też obliczyć szukaną sumę jako 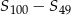dla wyjściowego ciągu.
Odpowiedź: