/Szkoła średnia/Ciągi/Arytmetyczny/Dany przez kolejne wyrazy

Zadanie nr 5488376

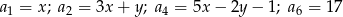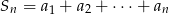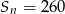W ciągu arytmetycznym mamy dane a1 = x ; a2 = 3x + y ; a4 = 5x − 2y− 1; a 6 = 17 . Niech Sn = a 1 + a2 + ⋅⋅⋅+ an . Dla jakich n zachodzi równość Sn = 260 ?

Wersja PDF

Rozwiązanie

Jeżeli oznaczymy różnicę ciągu przez r to mamy układ równań

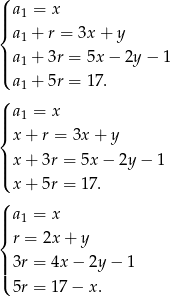
( ||| a1 = x { a1 + r = 3x + y | ||( a1 + 3r = 5x − 2y − 1 a1 + 5r = 17 . ( ||| a1 = x { x + r = 3x + y |||( x + 3r = 5x − 2y− 1 x + 5r = 1 7. ( || a1 = x |{ r = 2x + y ||| 3r = 4x − 2y− 1 ( 5r = 1 7− x .

Podstawiając z drugiego równania do trzeciego i czwartego dostajemy układ

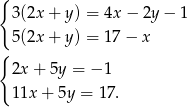
{ 3(2x + y) = 4x − 2y− 1 5(2x + y) = 1 7− x { 2x + 5y = − 1 11x + 5y = 17.

Odejmując od drugiego równania pierwsze mamy

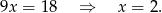
9x = 1 8 ⇒ x = 2.

Zatem  

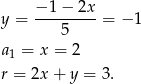
− 1− 2x y = ---------= −1 5 a1 = x = 2 r = 2x + y = 3.

Ze wzoru na sumę wyrazów ciągu arytmetycznego mamy równanie

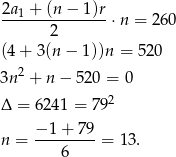
2a1-+-(n-−-1)r- 2 ⋅n = 260 (4+ 3(n − 1))n = 520 3n2 + n − 52 0 = 0 2 Δ = 6241 = 7 9 − 1+ 7 9 n = ---------= 13. 6

 
Odpowiedź: n = 13

Wersja PDF