Zadanie nr 5618141

Liczby

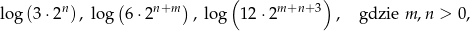
n ( n+m ) ( m+n +3) lo g(3 ⋅2 ) , log 6⋅ 2 , lo g 12⋅ 2 , gdzie m ,n > 0 ,

są odpowiednio pierwszym, piątym i dziewiątym wyrazem ciągu arytmetycznego. Wyznacz różnicę tego ciągu.

Rozwiązanie

Sposób I

Ze wzoru 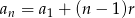an = a1 + (n − 1)r na -ty wyraz ciągu arytmetycznego mamy

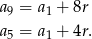
a = a + 8r 9 1 a5 = a1 + 4r.

Zatem

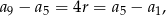
a9 − a 5 = 4r = a5 − a1,

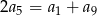czyli 2a5 = a1 + a9 . Mamy stąd równanie

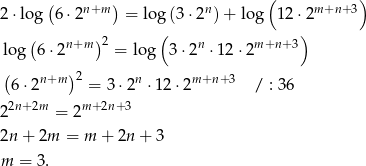
( ) ( ) 2⋅log 6 ⋅2n+m = log (3⋅ 2n)+ log 12⋅2m +n+ 3 ( ) log (6⋅ 2n+m )2 = lo g 3⋅ 2n ⋅1 2⋅2m +n+ 3 (6 ⋅2n+m )2 = 3 ⋅2n ⋅12 ⋅2m+n +3 / : 36 22n+2m = 2m+ 2n+ 3 2n + 2m = m + 2n + 3 m = 3.

To pozwala obliczyć różnicę ciągu.

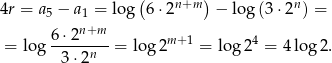
( n+m ) n 4r = a5 − a1 = lo g 6 ⋅2 − log (3⋅2 ) = 6 ⋅2n+m = log ------n- = log 2m+ 1 = log 24 = 4log 2. 3⋅2

Zatem 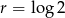r = log 2 .

Sposób II

Tak jak poprzednio zauważamy, że 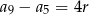a9 − a5 = 4r . Mamy zatem

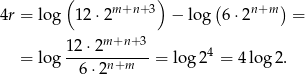
( ) 4r = log 12 ⋅2m +n+ 3 − lo g(6 ⋅2n+m ) = 12 ⋅2m +n+3 4 = log ------n+m---= lo g2 = 4log 2. 6⋅ 2

Stąd 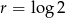r = log 2 .
Odpowiedź: log 2