/Szkoła średnia/Ciągi/Arytmetyczny/Dany przez kolejne wyrazy

Zadanie nr 9585335

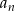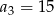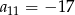Dany jest ciąg arytmetyczny an w którym a3 = 15 oraz a11 = − 1 7 .

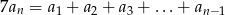  • Dla jakich n zachodzi równość 7an = a1 + a2 + a3 + ...+ an− 1 ?
  • Oblicz sumę pięćdziesięciu początkowych, ujemnych wyrazów ciągu 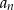an , które są podzielne przez 3.
Wersja PDF

Rozwiązanie

  • Wyznaczymy najpierw wzór na wyraz ogólny ciągu. Mamy układ równań
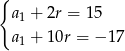
    { a + 2r = 15 1 a1 + 10r = − 17

    Odejmując od pierwszego równania drugie, mamy 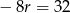− 8r = 32 , skąd 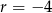r = − 4 i a1 = 23 .

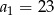    Musimy zatem rozwiązać równanie

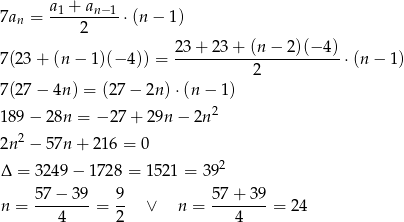
    a + a 7an = -1----n−1-⋅(n − 1) 2 23+--23-+-(n-−-2)(−-4)- 7(23 + (n − 1)(− 4)) = 2 ⋅(n − 1) 7(27 − 4n ) = (27− 2n) ⋅(n − 1) 189 − 28n = − 27 + 29n − 2n 2 2 2n − 57n + 216 = 0 Δ = 3249 − 1728 = 1521 = 392 n = 57−--39-= 9- ∨ n = 57-+-39-= 24 4 2 4

    Zatem n = 24 .  
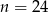    Odpowiedź: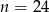 n = 24

  • Wyraz ogólny ciągu to 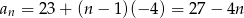an = 23 + (n − 1)(− 4) = 27− 4n . Widać stąd, że wyrazy ujemne to wyrazy dla 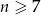n ≥ 7 . Ponieważ 27 dzieli się przez 3, to 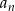an dzieli się przez 3 wtedy i tylko wtedy gdy n dzieli się przez 3, tzn. 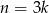n = 3k . Musimy zatem obliczyć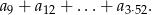
    a9 + a12 + ...+ a3⋅52.

    Liczby te tworzą ciąg arytmetyczny o różnicy 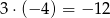3⋅(− 4) = − 12 . Mamy zatem

    S = a9 +-a156-⋅50 = (− 9− 5 97)⋅2 5 = − 15150 . 2

     
    Odpowiedź: -15150

Wersja PDF