/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy czworokątny

Zadanie nr 1405883

Dodaj do ulubionych
Dodaj do rozwiązanych

Graniastosłup prawidłowy czworokątny przecięto płaszczyzną, która zawiera krawędź podstawy oraz przechodzi przez środek przeciwległej krawędzi bocznej (zobacz rysunek).

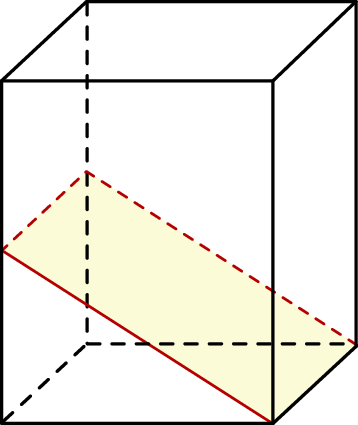
ZINFO-FIGURE

Oblicz jaki jest stosunek objętości dwóch brył na jakie został podzielony ten graniastosłup.

Rozwiązanie

Oznaczmy długość krawędzi podstawy graniastosłupa przez a , a jego wysokość przez 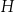H .

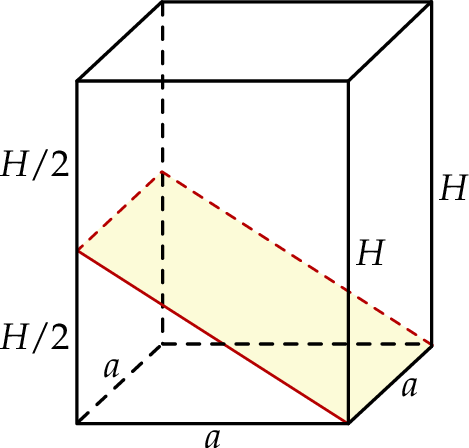
ZINFO-FIGURE

Objętość wyjściowego graniastosłupa jest równa

V = a2H .

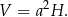
W wyniku podziału otrzymaliśmy dwie bryły – łatwo obliczyć objętość tej dolnej. Jest to graniastosłup trójkątny (który na rysunku leży na ścianie bocznej) o podstawie będącej trójkątem prostokątnym. Jego objętość jest równa

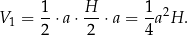
1 H 1 V1 = --⋅a⋅ --⋅a = -a2H . 2 2 4

W takim razie płaszczyzna podzieliła graniastosłup na bryły, których stosunek objętości jest równy

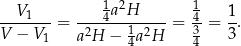
---V1-- ----14a2H----- 14- 1- V − V = a2H − 1a2H = 3 = 3. 1 4 4

 
Odpowiedź: 1 3

Wersja PDF