Zadanie nr 1934615
Kacper i Hela otrzymali identyczne zestawy 138 drewnianych klocków, w których każdy klocek jest sześcianem o krawędzi 2 cm. Kacper ze swoich klocków zbudował graniastosłup prawidłowy czworokątny i zostały mu dwa klocki, których nie było gdzie dołożyć. Hela ze swoich klocków zbudowała trzy identyczne graniastosłupy prawidłowe czworokątne i zostały jej trzy klocki, których nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej graniastosłupa zbudowanego przez Kacpra do pola powierzchni całkowitej jednego z graniastosłupów zbudowanych przez Helę. Wynik podaj w postaci ułamka nieskracalnego.
Rozwiązanie
Wiemy, że Kacper zbudował graniastosłup ze 136 klocków i graniastosłup ten nie miał jednego sześcianu w podstawie (bo wtedy dałoby się dołożyć pozostałe dwa klocki). Ponieważ 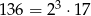 , graniastosłup w podstawie musiał mieć 4 klocki (liczba klocków w podstawie musi być kwadratem liczby naturalnej).
, graniastosłup w podstawie musiał mieć 4 klocki (liczba klocków w podstawie musi być kwadratem liczby naturalnej).
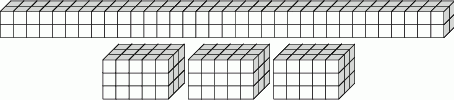
Na powierzchni tego graniastosłupa jest więc
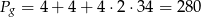
kwadratów o boku 2 cm.
Każdy z graniastosłupów zbudowanych przez Helę składa się z
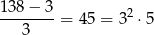
klocków, więc podobnie jak w przypadku Kacpra stwierdzamy, że musiał on mieć w podstawie 9 klocków. Na powierzchni takiego graniastosłupa jest więc
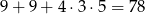
kwadratów o boku 2 cm. W takim razie interesujący nas stosunek powierzchni brył jest równy
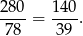
Odpowiedź: