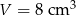/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy czworokątny

Zadanie nr 2180116

Dodaj do ulubionych
Dodaj do rozwiązanych

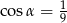Graniastosłup prawidłowy czworokątny przecięto płaszczyzną przechodzącą przez przekątną dolnej podstawy i jeden z wierzchołków górnej podstawy. Otrzymany przekrój jest trójkątem równoramiennym, którego ramiona tworzą kąt α , taki że cos α = 1 9 . Pole podstawy tego graniastosłupa wynosi 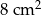8 cm 2 . Oblicz objętość tego graniastosłupa.

Rozwiązanie

Zaczynamy oczywiście od dużego rysunku.

PIC

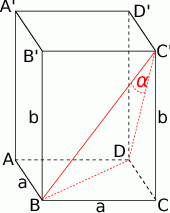
Znając pole dolnej podstawy, bez trudu wyliczamy krawędź a podstawy.

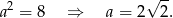
√ -- a2 = 8 ⇒ a = 2 2.

Pozostało wyliczyć krawędź boczną 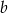b – zrobimy to pisząc twierdzenie cosinusów w trójkącie BDC ′ .

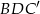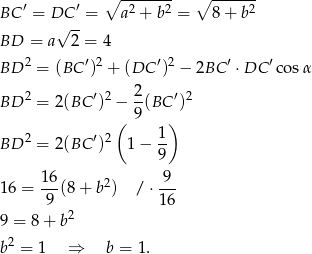
∘ ------- ∘ ------- BC ′ = DC ′ = a2 + b2 = 8+ b2 √ -- BD = a 2 = 4 BD 2 = (BC ′)2 + (DC ′)2 − 2BC ′ ⋅DC ′co sα BD 2 = 2(BC ′)2 − 2(BC ′)2 9 ( 1 ) BD 2 = 2(BC ′)2 1 − -- 9 16- 2 -9- 16 = 9 (8+ b ) / ⋅1 6 2 9 = 8 + b b2 = 1 ⇒ b = 1 .

Liczymy objętość

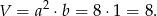
V = a2 ⋅b = 8 ⋅1 = 8.

 
Odpowiedź: V = 8 cm 3

Wersja PDF