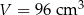/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy czworokątny

Zadanie nr 3711527

Przekątna graniastosłupa prawidłowego czworokątnego o długości 8 cm jest nachylona do płaszczyzny podstawy pod kątem 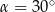α = 30∘ . Oblicz objętość tego graniastosłupa.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku.

PIC

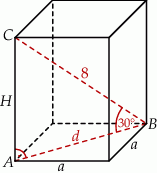
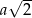Ponieważ przekątna kwadratu o boku a ma długość √ -- a 2 , patrząc na trójkąt prostokątny 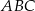ABC , mamy równanie

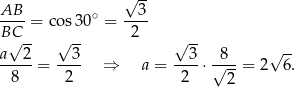
√ -- AB-- ∘ --3- BC = co s30 = 2 √ -- √ -- √ -- √ -- a--2-= --3- ⇒ a = --3-⋅√8--= 2 6. 8 2 2 2

Podobnie obliczamy wysokość 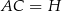AC = H .

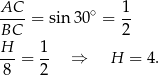
AC--= sin30 ∘ = 1- BC 2 H 1 -- = -- ⇒ H = 4 . 8 2

Objętość graniastosłupa jest więc równa

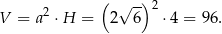
2 ( √ -) 2 V = a ⋅H = 2 6 ⋅4 = 9 6.

 
Odpowiedź: V = 96 cm 3

Wersja PDF