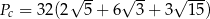/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy czworokątny

Zadanie nr 3823753

Przekątna prostopadłościanu ma długość 24 i tworzy z płaszczyzną jego podstawy kąt 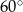60∘ . Jedna z krawędzi podstawy ma długość 8. Wyznacz objętość i pole powierzchni całkowitej tego prostopadłościanu.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku

PIC

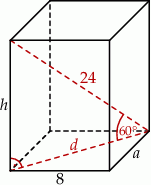
Zaczynamy od wyznaczenia długości przekątnej podstawy 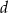d

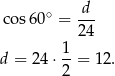
co s60∘ = d-- 24 1- d = 2 4⋅ 2 = 12.

Z twierdzenia Pitagorasa wyznaczamy długość drugiego boku podstawy

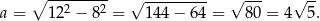
∘ --------- √ --------- √ --- √ -- a = 122 − 82 = 144 − 64 = 80 = 4 5.

Ponownie korzystając z funkcji trygonometrycznych wyznaczamy wysokość

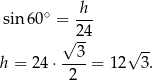
∘ h-- sin 60 = 24 √ -- √ -- h = 24 ⋅--3-= 1 2 3. 2

Teraz możemy już łatwo policzyć objętość

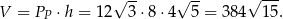
√ -- √ -- √ --- V = PP ⋅h = 12 3 ⋅8 ⋅4 5 = 384 15.

Policzenie pola całkowitego też nie sprawi problemu

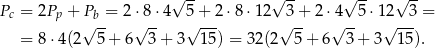
√ -- √ -- √ -- √ -- Pc = 2Pp + Pb = 2⋅ 8⋅4 5+ 2⋅8 ⋅12 3 + 2 ⋅4 5 ⋅12 3 = √ -- √ -- √ --- √ -- √ -- √ --- = 8 ⋅4(2 5 + 6 3 + 3 15) = 32(2 5 + 6 3+ 3 15).

 
Odpowiedź: 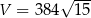√ --- V = 38 4 15 i √ -- √ -- √ --- Pc = 32(2 5 + 6 3 + 3 15 )

Wersja PDF