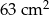/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy czworokątny

Zadanie nr 4599844

Graniastosłup prawidłowy czworokątny o krawędzi podstawy 6 cm przecięto płaszczyzną przechodzącą przez środki dwóch sąsiednich krawędzi podstawy. Płaszczyzna ta przecina trzy krawędzie boczne i jest nachylona do płaszczyzny podstawy pod kątem 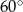60 ∘ . Zaznacz na rysunku ten przekrój i oblicz jego pole.

Wersja PDF

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

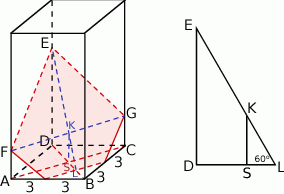
Z obrazka widać, że w przekroju otrzymamy pięciokąt, który jest sumą trapezu równoramiennego i trójkąta równoramiennego. Obliczmy wysokości tych figur. Z trójkąta prostokątnego 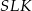SLK mamy

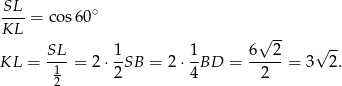
SL-- ∘ KL = co s60 √ -- √ -- KL = SL- = 2 ⋅ 1-SB = 2⋅ 1BD = 6--2-= 3 2. 12 2 4 2

Teraz stosujemy twierdzenie Talesa w trójkącie DLE .

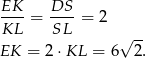
EK-- DS-- KL = SL = 2 √ -- EK = 2 ⋅KL = 6 2.

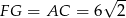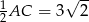Podstawy trapezu mają długości √ -- FG = AC = 6 2 i 1 √ -- 2AC = 3 2 , więc jego pole jest równe

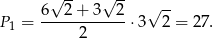
√ -- √ -- 6--2-+-3--2- √ -- P 1 = 2 ⋅3 2 = 27.

Pole trójkąta FGE jest równe

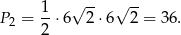
√ -- √ -- P = 1-⋅6 2 ⋅6 2 = 36. 2 2

Zatem pole interesującego nas przekroju jest równe

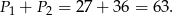
P1 + P2 = 2 7+ 36 = 63.

 
Odpowiedź: 63 cm 2

Wersja PDF