Zadanie nr 6403788
Graniastosłup prawidłowy czworokątny o krawędzi podstawy równej  i wysokości dwa razy dłuższej od krawędzi podstawy, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem miary
i wysokości dwa razy dłuższej od krawędzi podstawy, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem miary 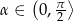 . Oblicz pole otrzymanego przekroju. Rozważ wszystkie możliwe przypadki.
. Oblicz pole otrzymanego przekroju. Rozważ wszystkie możliwe przypadki.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
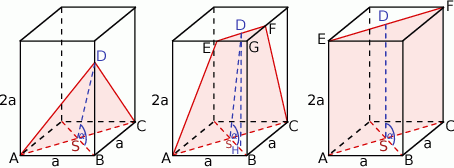
Z obrazka widać, że w zależności od miary kąta  , otrzymany przekrój może być trójkątem równoramiennym, trapezem lub prostokątem.
, otrzymany przekrój może być trójkątem równoramiennym, trapezem lub prostokątem.
Od razu załatwmy przypadek prostokąta (czyli przypadek 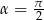 ). Pole tego prostokąta jest równe
). Pole tego prostokąta jest równe
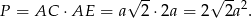
Łatwo też jest w przypadku trójkąta równoramiennego. Jego podstaw ma długość 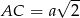 , a wysokość
, a wysokość 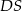 możemy obliczyć z trójkąta prostokątnego
możemy obliczyć z trójkąta prostokątnego 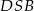 .
.

Pole trójkąta jest więc równe
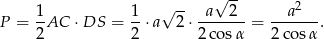
Zauważmy jeszcze, że ten przypadek będzie zachodził, o ile
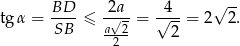
No i został najciekawszy przypadek, gdy przekrój jest trapezem równoramiennym. Dolna podstawa tego trapezu to 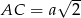 . Aby obliczyć jego wysokość
. Aby obliczyć jego wysokość 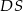 oznaczmy przez
oznaczmy przez 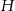 rzut punktu
rzut punktu 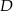 na podstawę graniastosłupa. W trójkącie
na podstawę graniastosłupa. W trójkącie 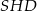 mamy
mamy
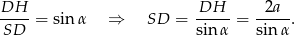
Aby obliczyć długość górnej podstawy trapezu zauważmy, że trójkąt 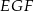 jest połówką kwadratu, więc
jest połówką kwadratu, więc
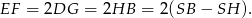
Ponadto
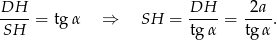
Mamy zatem
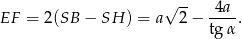
Pole trapezu jest więc równe
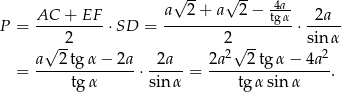
Odpowiedź: