/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy czworokątny

Zadanie nr 7146780

Dodaj do ulubionych
Dodaj do rozwiązanych

W graniastosłupie prawidłowym czworokątnym o objętości równej 108 stosunek długości krawędzi podstawy do wysokości graniastosłupa jest równy 14 . Przekątna tego graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem α (zobacz rysunek).

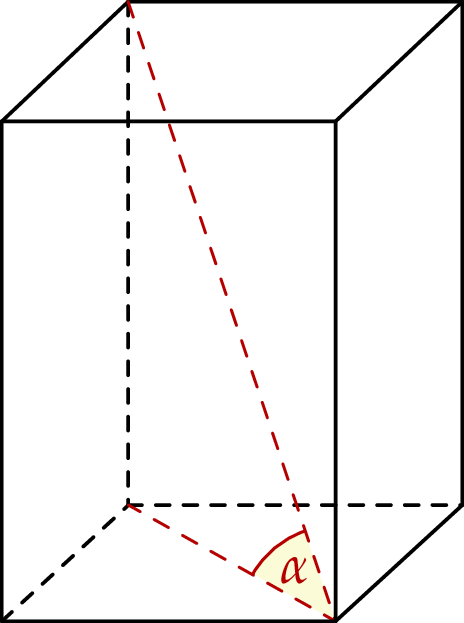
ZINFO-FIGURE

Oblicz cosinus kąta α oraz pole powierzchni całkowitej tego graniastosłupa.

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.