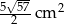/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy czworokątny

Zadanie nr 9270961

Dodaj do ulubionych
Dodaj do rozwiązanych

W graniastosłupie prawidłowym czworokątnym krawędź podstawy ma długość 5 cm, a krawędź boczna ma długość 4 cm. Przez wierzchołek górnej podstawy i przekątną dolnej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju. Rozpatrz 2 przypadki.

Rozwiązanie

Gdy naszkicujemy sobie opisaną sytuację to jest jasne jakie są dwa przypadki.

PIC

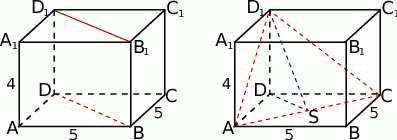
W przypadku przekroju 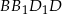BB 1D1D sprawa jest prosta – jest to prostokąt o bokach długości 4 i 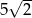√ -- 5 2 , zatem jego pole wynosi

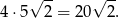
√ -- √ -- 4⋅ 5 2 = 20 2 .

Zajmijmy się teraz przekrojem 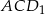ACD 1 . Jest to trójkąt równoramienny o podstawie 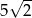√ -- 5 2 . Wyliczymy jego wysokość D1S .

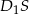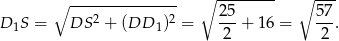
∘ -------- ∘ --- ∘ --------------- 25 57 D 1S = DS 2 + (DD 1)2 = ---+ 16 = ---. 2 2

Zatem pole przekroju wynosi

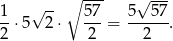
√ -- ∘ --- √ --- 1-⋅5 2 ⋅ 57-= 5--57. 2 2 2

 
Odpowiedź: 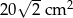√ -- 20 2 cm 2 lub √-- 5-527-cm 2

Wersja PDF