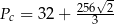/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy czworokątny

Zadanie nr 9636220

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole podstawy graniastosłupa prawidłowego czworokątnego jest równe 16. Przekątna graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem, którego sinus jest równy 45 . Oblicz pole powierzchni całkowitej tego graniastosłupa.

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

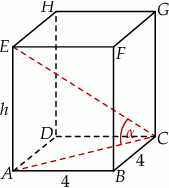
Z podanego pola podstawy wiemy, że w podstawie graniastosłupa jest kwadrat o boku 4. Przekątna tego kwadratu ma więc długość 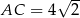√ -- AC = 4 2 .

Oznaczmy przez 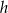h długość wysokości graniastosłupa. Z podanego sinusa kąta α między przekątną graniastosłupa, a płaszczyzną podstawy mamy

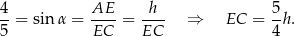
4 AE h 5 --= sin α = ---- = ---- ⇒ EC = --h. 5 EC EC 4

Piszemy teraz twierdzenie Pitagorasa w trójkącie prostokątnym 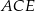ACE .

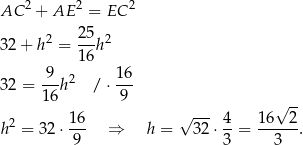
2 2 2 AC + AE = EC 2 25-2 32 + h = 16h 9 16 32 = --h 2 / ⋅--- 16 9 √ -- 2 16- √ --- 4- 16--2- h = 3 2⋅ 9 ⇒ h = 32⋅ 3 = 3 .

Pozostało obliczyć pole powierzchni całkowitej graniastosłupa.

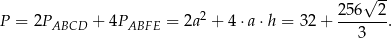
√ -- 2 256--2- P = 2PABCD + 4PABFE = 2a + 4 ⋅a ⋅h = 32 + 3 .

 
Odpowiedź: √ - P = 3 2+ 256--2 c 3

Wersja PDF