Zadanie nr 9760663
Kąt między przekątnymi sąsiednich ścian bocznych prostopadłościanu o podstawie kwadratowej jest równy 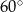 . Krawędź podstawy ma długość 12. Wyznacz pole powierzchni całkowitej tego prostopadłościanu i kąt nachylenia przekątnej ściany bocznej do płaszczyzny podstawy prostopadłościanu.
. Krawędź podstawy ma długość 12. Wyznacz pole powierzchni całkowitej tego prostopadłościanu i kąt nachylenia przekątnej ściany bocznej do płaszczyzny podstawy prostopadłościanu.
Rozwiązanie
Zaczynamy od rysunku
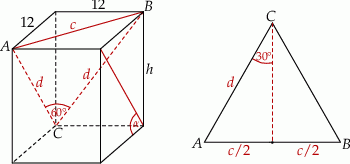
Ponieważ podstawą jest kwadrat, więc ścianami bocznymi są identyczne prostokąty. Z twierdzenia Pitagorasa obliczamy długość przekątnej 
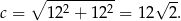
Przekątne dwóch sąsiadujących ścian są sobie równe, więc trójkąt 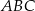 jest równoramienny. Zatem stosując funkcje trygonometryczne możemy obliczyć długość
jest równoramienny. Zatem stosując funkcje trygonometryczne możemy obliczyć długość 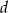
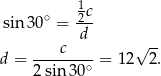
Mogliśmy też długość odcinka 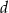 obliczyć szybciej: wystarczyło zauważyć, że trójkąt
obliczyć szybciej: wystarczyło zauważyć, że trójkąt 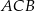 jest równoramienny z kątem między ramionami równym
jest równoramienny z kątem między ramionami równym 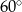 . Jest to więc trójkąt równoboczny i
. Jest to więc trójkąt równoboczny i
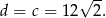
Zatem nasz prostopadłościan jest sześcianem o krawędzi równej 12. Teraz już łatwo obliczyć pole całkowite
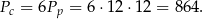
Ponieważ 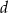 jest przekątną kwadratu, więc kąt między nią, a podstawą jest równy
jest przekątną kwadratu, więc kąt między nią, a podstawą jest równy
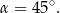
Odpowiedź: 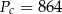 i
i