/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy czworokątny

Zadanie nr 9764619

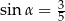W graniastosłupie czworokątnym prawidłowym przekątna o długości 5 jest nachylona do płaszczyzny podstawy pod kątem α takim, że sinα = 35 . Wyznacz objętość tego graniastosłupa.

Wersja PDF

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

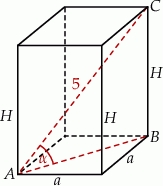
Z rysunku widać, że łatwo obliczyć wysokość graniastosłupa:

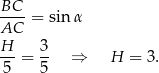
BC--= sinα AC H- 3- 5 = 5 ⇒ H = 3 .

Pozostało obliczyć krawędź a podstawy.

Sposób I

Obliczamy 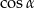cosα z jedynki trygonometrycznej.

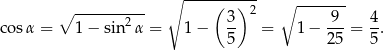
∘ ----(--)-- ∘ ------- ∘ -------2-- 3 2 9 4 c osα = 1− sin α = 1− 5- = 1 − 25-= 5-.

Mamy więc

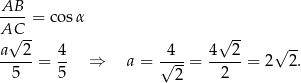
AB ---- = cos α AC√ -- √ -- a---2 4- -4-- 4--2- √ -- 5 = 5 ⇒ a = √ 2-= 2 = 2 2.

Zatem objętość graniastosłupa jest równa

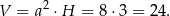
V = a2 ⋅H = 8⋅ 3 = 24.

Sposób II

Korzystamy z twierdzenia Pitagorasa w trójkącie prostokątnym ABC .

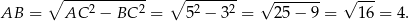
∘ ---2------2- ∘ -2----2 √ ------- √ --- AB = AC − BC = 5 − 3 = 25− 9 = 16 = 4 .

Stąd

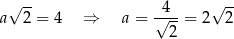
√ -- 4 √ -- a 2 = 4 ⇒ a = √---= 2 2 2

i objętość graniastosłupa jest równa

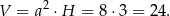
2 V = a ⋅H = 8⋅ 3 = 24.

 
Odpowiedź: 24

Wersja PDF