/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy czworokątny

Zadanie nr 9857509

Dodaj do ulubionych
Dodaj do rozwiązanych

Objętość graniastosłupa prawidłowego czworokątnego jest równa 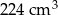3 224 cm , a promień okręgu opisanego na podstawie ma długość 4 cm. Wyznacz miarę kąta między przekątnymi sąsiednich ścian bocznych wychodzącymi z tego samego wierzchołka graniastosłupa. Wynik podaj z dokładnością do ∘ 1 .

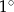Rozwiązanie

Oznaczmy długość krawędzi podstawy graniastosłupa przez a , a długość krawędzi bocznej przez 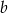b .

PIC

Promień okręgu opisanego na podstawie to po prostu połowa długości przekątnej podstawy, więc mamy

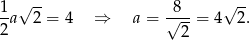
-- -- 1a√ 2 = 4 ⇒ a = √8--= 4√ 2 . 2 2

Z podanej objętości możemy teraz obliczyć wysokość graniastosłupa.

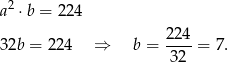
a2 ⋅b = 22 4 224 32b = 224 ⇒ b = ----= 7. 32

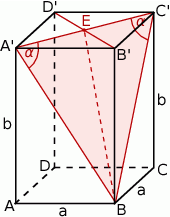
Zastanówmy się teraz jak obliczyć interesujący nas kąt 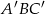′ ′ A BC . Trójkąt 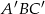′ ′ A BC jest równoramienny, więc oczywiście wystarczy obliczyć

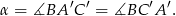
α = ∡BA ′C ′ = ∡BC ′A ′.

To jednak jest dość proste, bo cosinus tego kąta możemy obliczyć z trójkąta prostokątnego 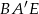BA ′E . Obliczamy najpierw BA ′ .

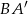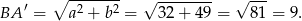
∘ ------- √ -------- √ --- BA ′ = a2 + b2 = 32 + 49 = 8 1 = 9.

W takim razie

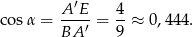
′ cosα = A-E- = 4-≈ 0,44 4. BA ′ 9

Teraz odczytujemy z tablic, że 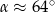∘ α ≈ 64 . Zatem interesujący na kąt między przekątnymi ścian bocznych ma miarę

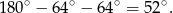
180 ∘ − 64 ∘ − 6 4∘ = 52∘.

 
Odpowiedź: 52∘

Wersja PDF