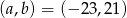/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą/Przez stopnia 2

Zadanie nr 1119010

Wielomian 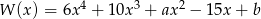4 3 2 W (x) = 6x + 10x + ax − 15x + b jest podzielny przez trójmian 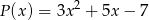P (x) = 3x 2 + 5x − 7 . Wyznacz liczby a i b .

Wersja PDF

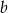Rozwiązanie

Dzielimy z resztą wielomian 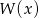W (x) przez wielomian 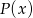P (x) . My zrobimy to grupując wyrazy.

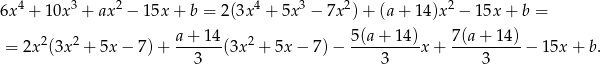
4 3 2 4 3 2 2 6x + 10x + ax − 1 5x+ b = 2(3x + 5x − 7x )+ (a+ 1 4)x − 15x + b = a+ 14 5(a+ 14) 7(a+ 14) = 2x2(3x 2 + 5x − 7)+ ------(3x 2 + 5x − 7)− ---------x + ----------− 15x + b. 3 3 3

Wiemy, że wielomian 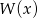W (x ) dzieli się przez 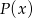P(x ) , więc otrzymana reszta musi być wielomianem zerowym.

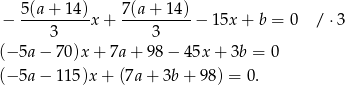
5(a-+-14-) 7(a-+-14)- − 3 x + 3 − 1 5x+ b = 0 / ⋅ 3 (− 5a − 70)x + 7a+ 98− 45x + 3b = 0 (− 5a − 115 )x+ (7a+ 3b+ 98) = 0.

Mamy stąd 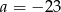a = − 23 oraz

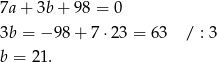
7a + 3b + 98 = 0 3b = −9 8+ 7⋅23 = 63 / : 3 b = 2 1.

 
Odpowiedź: (a,b) = (− 23 ,21)

Wersja PDF