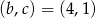Zadanie nr 5916002
Wielomian 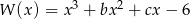 jest podzielny przez trójmian kwadratowy
jest podzielny przez trójmian kwadratowy 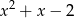 . Wyznacz współczynniki
. Wyznacz współczynniki 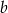 i
i  wielomianu
wielomianu 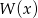 .
.
Rozwiązanie
Rozłóżmy podany trójmian kwadratowy na czynniki.
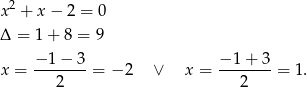
Zatem 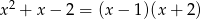 .
.
Jeżeli dany wielomian trzeciego stopnia ma się dzielić przez 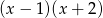 to musi się jednocześnie dzielić przez
to musi się jednocześnie dzielić przez 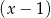 i
i 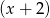 , a to oznacza, że liczby 1 i
, a to oznacza, że liczby 1 i 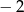 muszą być jego pierwiastkami. Daje to nam układ równań
muszą być jego pierwiastkami. Daje to nam układ równań
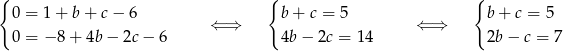
Dodając równania stronami (żeby zredukować  ) mamy
) mamy 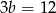 , czyli
, czyli 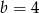 . Stąd
. Stąd 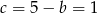 .
.
Odpowiedź: