/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą/Przez stopnia 2

Zadanie nr 7260978

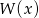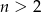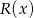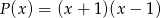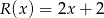Dany jest wielomian W (x) stopnia n > 2 , którego suma wszystkich współczynników jest równa 4, a suma współczynników przy potęgach o wykładnikach nieparzystych jest równa sumie współczynników przy potęgach o wykładnikach parzystych. Wykaż, że reszta R(x ) z dzielenia tego wielomianu przez wielomian P(x) = (x + 1)(x− 1) jest równa R (x) = 2x + 2 .

Wersja PDF

Rozwiązanie

Suma współczynników wielomianu

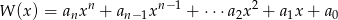
n n− 1 2 W (x) = anx + an−1x + ⋅⋅⋅a2x + a1x + a0

to po prostu wartość 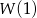W (1) . Ponadto, z informacji o sumach współczynników przy potęgach parzystych i nieparzystych wynika, że 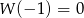W (− 1) = 0 . Wiemy zatem, że

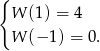
{ W (1) = 4 W (− 1) = 0.

Reszta 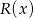R (x) z dzielenia przez przez wielomian 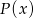P (x) stopnia 2 jest wielomianem stopnia 1, więc ma postać 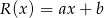R (x) = ax + b . Mamy zatem równość

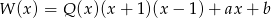
W (x) = Q (x)(x + 1)(x − 1) + ax + b

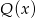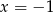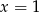dla pewnego wielomianu Q (x) . Podstawiając w tej równości x = − 1 i x = 1 otrzymujemy

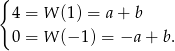
{ 4 = W (1) = a+ b 0 = W (− 1) = −a + b.

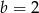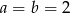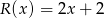Dodając równania tego układu stronami mamy b = 2 . Stąd a = b = 2 , co dowodzi, że R (x) = 2x + 2 .

Wersja PDF