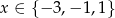Zadanie nr 9488344
Reszta z dzielenia wielomianu 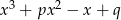 przez trójmian
przez trójmian 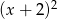 wynosi
wynosi 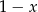 . Wyznacz pierwiastki tego wielomianu.
. Wyznacz pierwiastki tego wielomianu.
Rozwiązanie
Sposób I
Podzielmy podany wielomian przez 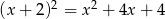 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
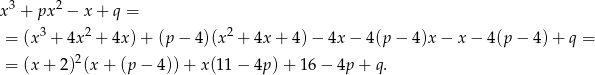
Ponieważ reszta ma być równa 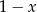 mamy
mamy 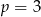 i
i
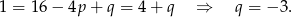
Zatem nasz wielomian to
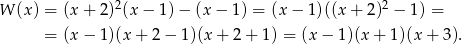
Sposób II
Z podanych informacji wiemy, że
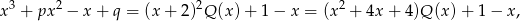
dla pewnego wielomianu 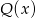 . Ponieważ lewa strona jest wielomianem stopnia 3,
. Ponieważ lewa strona jest wielomianem stopnia 3, 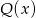 jest wielomianem liniowym.
jest wielomianem liniowym.
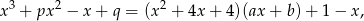
Patrząc na wpółczynnik przy 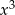 po obu stronach równania mamy
po obu stronach równania mamy 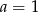 , a patrząc na współczynnik przy
, a patrząc na współczynnik przy  mamy
mamy
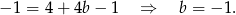
Mamy zatem
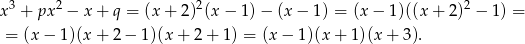
Odpowiedź: