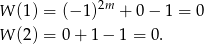/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą/Przez stopnia 2

Zadanie nr 9902032

Wykaż, że wielomian 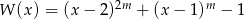2m m W (x) = (x − 2) + (x − 1) − 1 jest podzielny przez wielomian 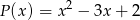P(x) = x 2 − 3x + 2 dla każdego m ∈ N + .

Wersja PDF

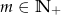Rozwiązanie

Zobaczmy jakie pierwiastki ma wielomian przez który dzielimy.

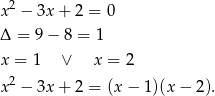
2 x − 3x + 2 = 0 Δ = 9 − 8 = 1 x = 1 ∨ x = 2 x 2 − 3x + 2 = (x− 1)(x − 2).

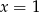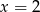Na mocy twierdzenia Bézout wystarczy sprawdzić czy liczby x = 1 i x = 2 są pierwiastkami podanego wielomianu. Sprawdzamy.

W (1) = (− 1 )2m + 0− 1 = 0 W (2) = 0 + 1 − 1 = 0.
Wersja PDF