Zadanie nr 2052544
Uzasadnij, że liczby 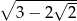 i
i 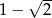 są liczbami przeciwnymi.
są liczbami przeciwnymi.
Rozwiązanie
Sposób I
Musimy pokazać, że
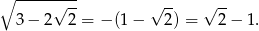
Ponieważ obie strony są dodatnie, możemy równość podnieść stronami do kwadratu.
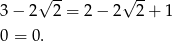
Tak więc liczby rzeczywiście są równe.
Sposób II
Liczymy
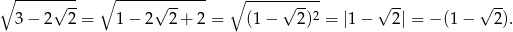
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Uzasadnij, że liczby 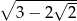 i
i 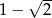 są liczbami przeciwnymi.
są liczbami przeciwnymi.
Sposób I
Musimy pokazać, że
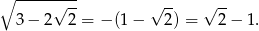
Ponieważ obie strony są dodatnie, możemy równość podnieść stronami do kwadratu.
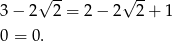
Tak więc liczby rzeczywiście są równe.
Sposób II
Liczymy