/Szkoła średnia/Liczby/Potęgi i pierwiastki/Udowodnij...

Zadanie nr 2918618

Dodaj do ulubionych
Dodaj do rozwiązanych

Uzasadnij, że liczba 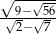√ 9−√-56 -√2−-√7- jest liczbą całkowitą.

Rozwiązanie

Sposób I

Oznaczmy 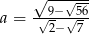------ √ 9−√ 56 a = -√2−√-7- . Mamy wtedy

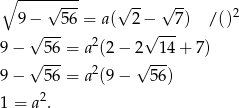
∘ ----√---- √ -- √ -- 9 − 56 = a ( 2− 7) /()2 √ --- 2 √ --- 9− 56 = a (2 − 2 14 + 7) √ --- 2 √ --- 9− 56 = a (9 − 56) 1 = a2.

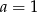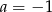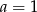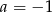W takim razie a = 1 lub a = − 1 . W obu przypadkach jest to liczba całkowita. Gdybyśmy jednak chcieli wiedzieć, czy a = 1 czy a = − 1 to wystarczy zauważyć, że 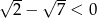√ -- √ -- 2− 7 < 0 , więc a < 0 .

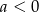Sposób II

Spróbujemy znaleźć pod pierwiastkiem kwadrat różnicy (jak to zrobić sugerują pozostałe pierwiastki).

------------- ∘ ----√---- ∘ -----√-------- ∘ √ -- √ --2 --9-−---56- --7-−-2--1-4+-2- ---(--7−----2)- √ -- √ -- = √ -- √ -- = √ -- √ -- = 2 −√ --7 √ -- √ 2-− √ 7- 2 − 7 |--7−----2| --7-−---2- = √ 2− √ 7-= √ 2-− √ 7-= − 1.
Wersja PDF