Zadanie nr 5637969
Wykaż, że dla dowolnej liczby całkowitej  liczba
liczba 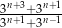 jest liczbą całkowitą.
jest liczbą całkowitą.
Rozwiązanie
Przekształcamy ułamek wyciągając w liczniku i w mianowniku 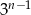 przed nawias.
przed nawias.
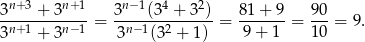
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla dowolnej liczby całkowitej  liczba
liczba 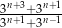 jest liczbą całkowitą.
jest liczbą całkowitą.
Przekształcamy ułamek wyciągając w liczniku i w mianowniku 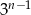 przed nawias.
przed nawias.